边界层理论
边界层理论
关键词:边界层 增长比率 y+
疑问:
- 边界层应该画多少个(N)?
- 第一层网格的大小(yH)?
- 增长比率是多少(G)?
1、边界层理论
流体在大雷诺数下作绕流流动时,在离固体壁面较远处,粘性力比惯性力小得多,可以忽略;但在固体壁面附近的薄层中,粘性力的影响则不能忽略,沿壁面法线方向存在相当大的速度梯度,这一薄层叫做边界层。流体的雷诺数越大,边界层越薄。
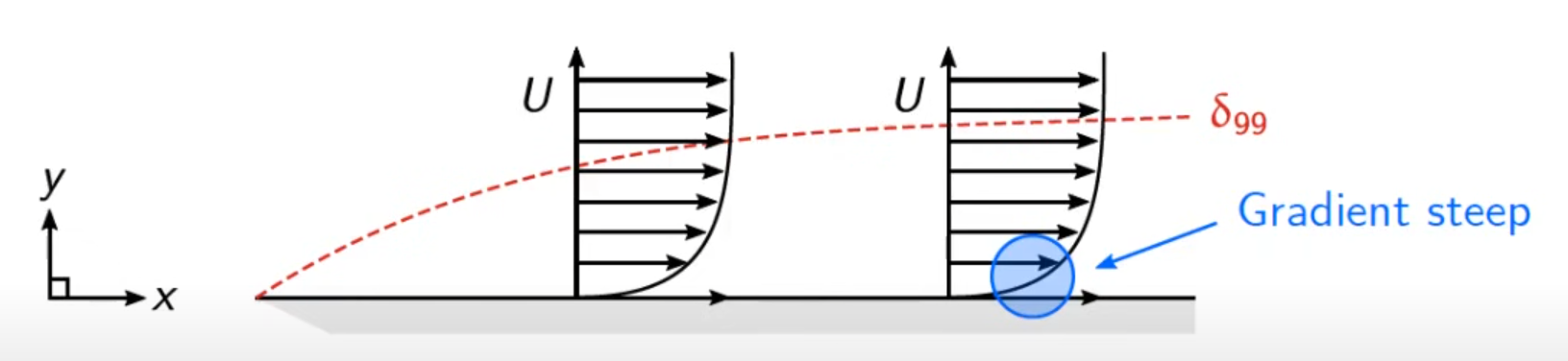
需要小的单元来捕获给定方向上的梯度。
\({\delta_{99}}\)表示速度到达自由流速度 99%时厚度。
- 在边界层内,粘性力与惯性力同一数量级
- 由于边界层很薄,可以近似认为边界层中各截面上的压强等于同一截面上边界层外边界上的压强值。
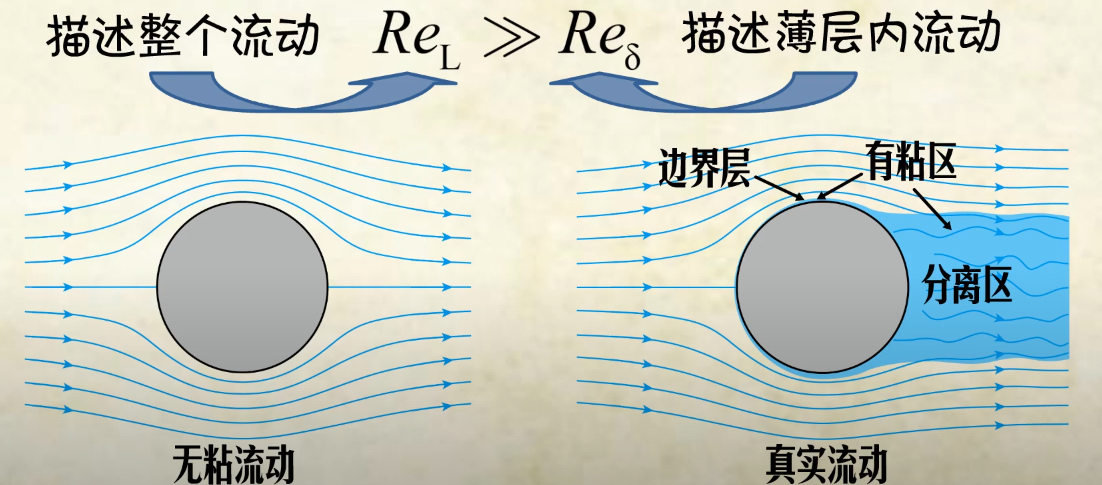
无粘流动与真实流动的区别
考虑边界层的存在,在后方会出现分离区
2、第一层网格大小
yH 依赖于 y+的值
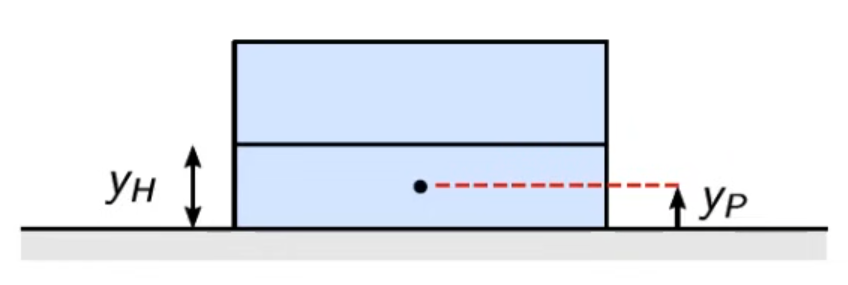
\[y^+=\frac{\rho u_\tau y_p}\mu \]
- 动力粘度:单位为 Pa.s(N/m2.s),厘泊(CP),1Pa.s=10P(泊)=1000CP(厘泊)
- 运动粘度 V:即动力粘度 u 与密度 p 的比值:v=u/p,运动粘度的单位为 m2/s,习惯单位为:厘斯(mm2/s)
- 这里指的是动力粘度
3、总高度
网格边界层的总高度要包含\({\delta_{99}}\)
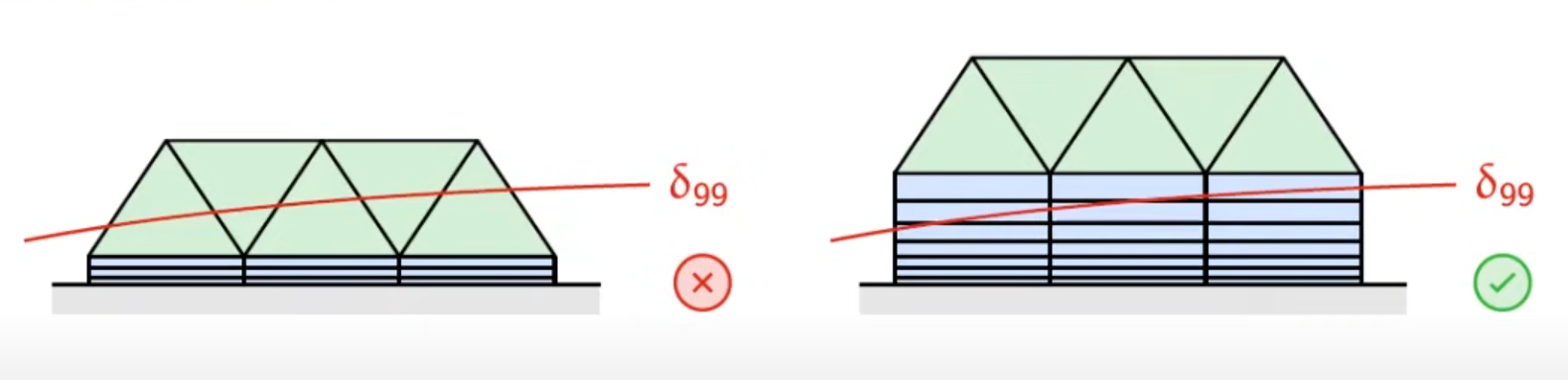
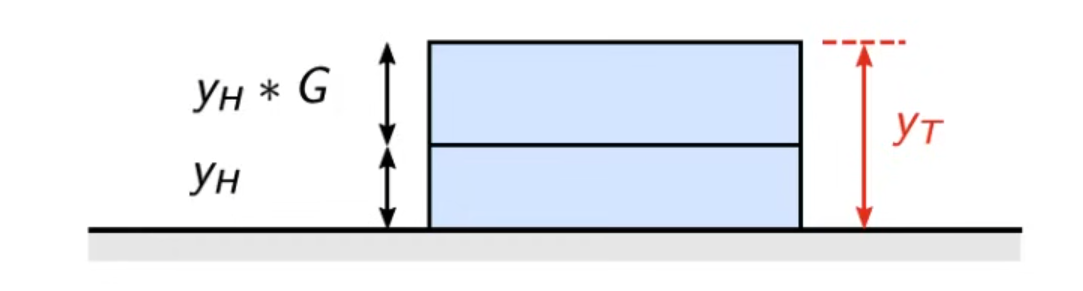
2 个边界层
\[y_T=y_H+y_H*G\]
3 个边界层
\[y_T=y_H+y_HG+y_HG^2\]
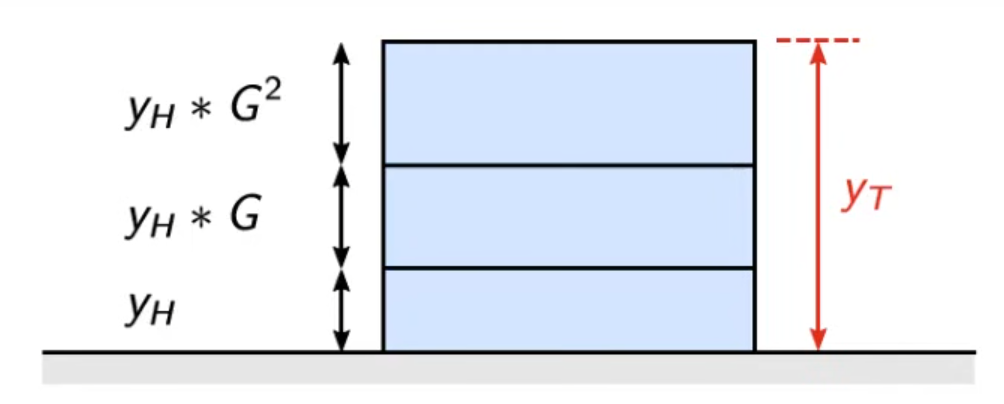
我们可以得出边界层公式
\[y_T=y_H+y_HG+y_HG^2+y_HG^3+...+y_HG^{N-1}\]
即
\[\sum_{k=0}^{N-1}y_HG^k=y_H\frac{1-G^N}{1-G}\]
\[\delta_{99}=y_H\frac{1-G^N}{1-G}\]
而边界层厚度的计算公式为
\[\begin{aligned}\delta_{99}&=\frac{4.91L}{\sqrt{Re_L}}\quad&Re<5\times10^5\\\delta_{99}&=\frac{0.38L}{Re_L^{1/5}}\quad&Re>5\times10^5\end{aligned}\]
4、G 和 N 如何确定
首先可以大致猜测一下
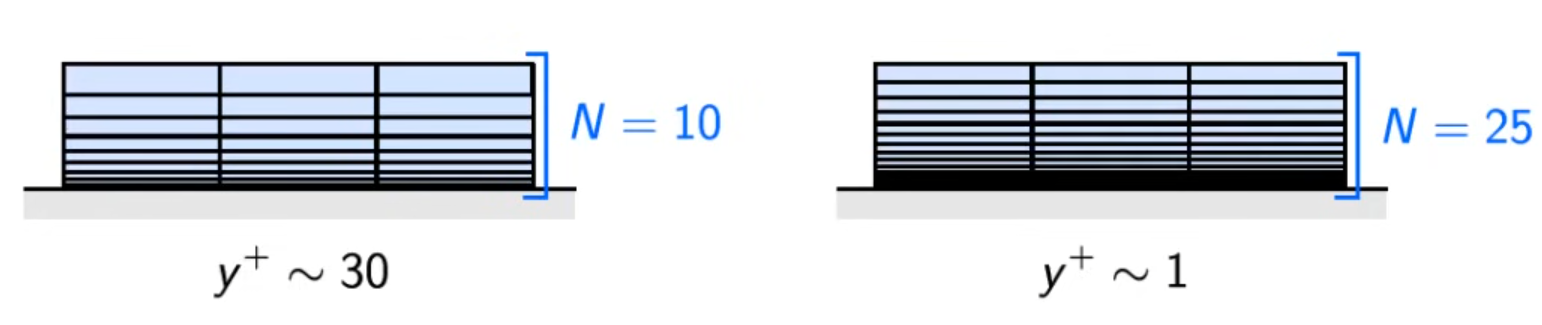
如果 N>10,则第一个网格高度约为 30
如果 N>25,则第一个网格高度约为 1
通常
- 1.05<G<1.3
- 10<N<30
5、如何确定网格是好坏
小的网格转变

在大涡模拟中
\[v_{sgs}=\left(C_{s}\Delta\right)^{2}\sqrt{2S_{ij}S_{ij}}\]
网格大小突然改变,会导致\(v_{sgs}\)突然改变
在 RANS 中
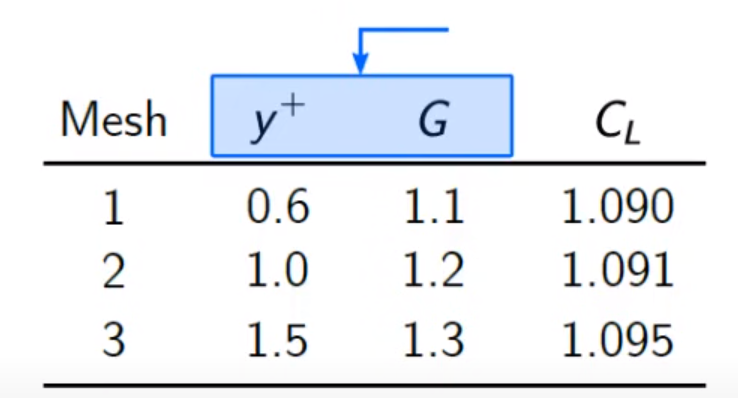
使用至少 3 种不同的网格进行网格细化研究是非常必要的。
附录
y+定义
根据 y+的大小,可以将湍流边界层分为好多层。
- 粘性子层(\(y^{+} < 5\)):粘性影响占据主要地位,雷诺应力可忽略,则\(u^{+} = y^{+}\)
- 对数区域(\(y^{+} > 30\)):湍流应力占主导地位,\(u^+=\frac1\kappa ln(y^+)+B\),其中 k=0.41,B=5.2
- 缓冲层(\(5 < y^{+} < 30\)):粘性应力和湍流应力的大小相近,由于该区域比较复杂,速度剖面的定义不明确,原始壁面函数会避开位于该区域的第一个单元中心。
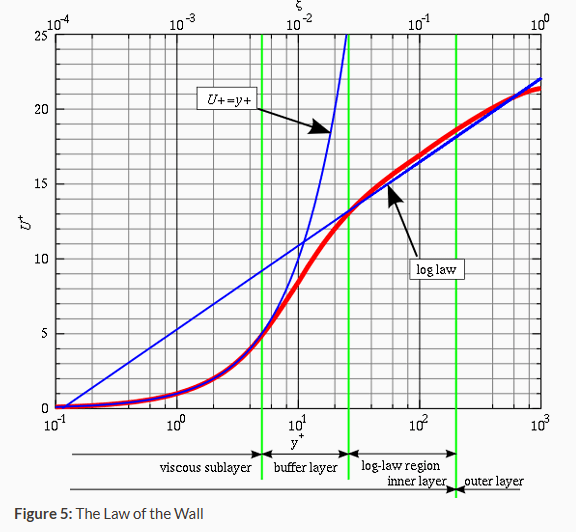
壁面函数要求第一层网格尺寸\(30<y^{+}<300\)
