Fluent 中的浮力模型

1、基本概念

当计算域开启重力场和能量场时，可在ke模型中考虑浮力的产生。

由于浮力而产生的湍流公式：

\[G_b=\beta g_i\frac{\mu_t}{\mathrm{Pr}_t}\frac{\partial T}{\partial x_i}\]

其中\(Pr_{t}\)是能量的湍流普朗特数，\(g_{i}\)是重力矢量在\(i\)方向上的分量。对于标准和可实现ke模型，\(Pr_{t}=0.85\)。在RNG ke模型，$Pr_{t}= \(。其中\)$由以下公式计算：

\[\left|\frac{\alpha-1.3929}{\alpha_0-1.3929}\right|^{0.6321}\left|\frac{\alpha+2.3929}{\alpha_0+2.3929}\right|^{0.3679}=\frac{\mu_{\mathrm{mol}}}{\mu_{\mathrm{eff}}}\]

其中\(\alpha_{0}=1.0\)，在高雷诺数限制下，\(\mu_{\mathrm{mol}}/\mu_{\mathrm{eff}}\ll1\)，\(\alpha_{k}=\alpha_{\epsilon}\approx1.393\)

系数$$定义为

\[\beta=-\frac1\rho\left(\frac{\partial\rho}{\partial T}\right)_p\]

对于理想气体状态方程：

\[G_b=-g_i\frac{\mu_t}{\rho\mathrm{Pr}_t}\frac{\partial\rho}{\partial x_i}\]

在不稳定分层中，湍动能趋于增大。对于不稳定的分层，浮力会抑制湍流。

受浮力影响程度由常数\(C_{3\epsilon }\)决定，在 Fluent 中可通过以下公式计算

\[C_{3\epsilon}=\tanh\left|\frac{v}{u}\right|\]

\(v\)是平行于重力矢量的流速分量，\(u\)是垂直于重力矢量的流速分量。对于主流方向与重力方向一致的浮力剪切层，该常数为 1。对于垂直于重力矢量的浮力剪切层，该值为 0。

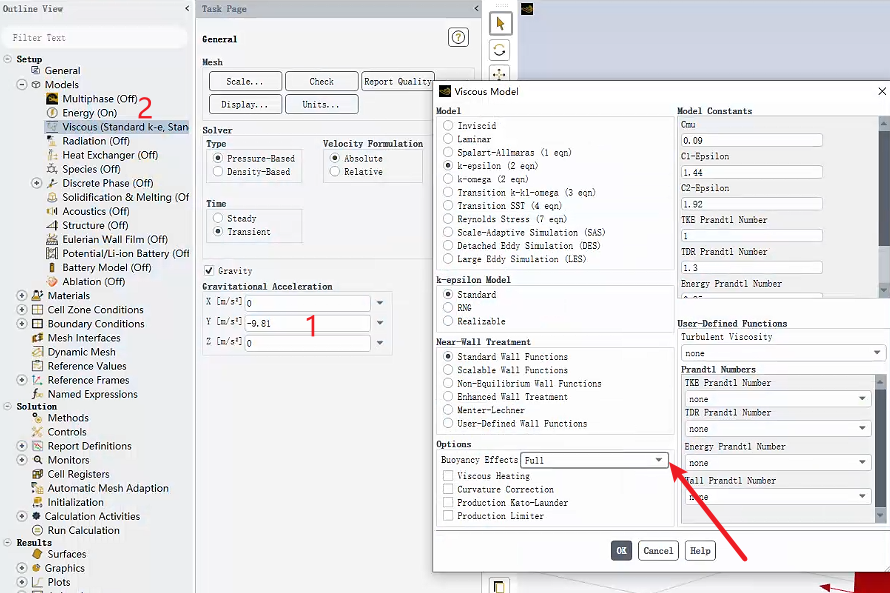
2、如何操作

开启重力加速度和能量方程，即可在ke模型中设置全浮力模型。