深度学习入门

基本配置

github

学习视频地址

环境配置

  1. 在 anaconda 中新建虚拟环境conda create -n Pytorch python=3.9
  2. 激活虚拟环境并安装 numpy、matplotlib、pandas 库
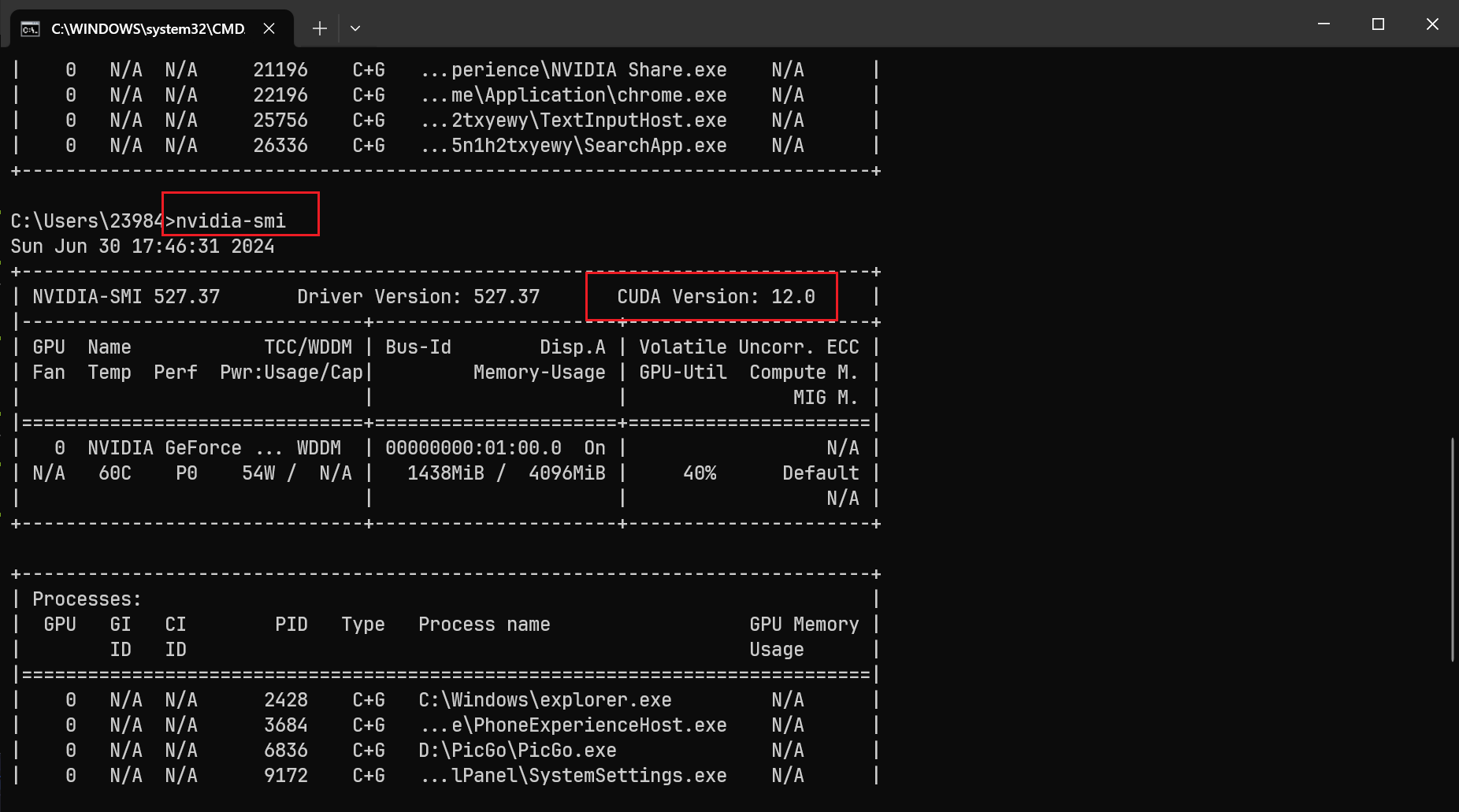
  3. 在终端命令行输入：nvidia-smi查看 CUNDA 版本，在安装 pytorch 时需要注意版本：CONDA > conda

更改 jupyter 默认打开目录

  1. 首先使用以下命令生成 jupyter 配置文件，生成的文件一般在C:\Users\用户名\.jupyter文件夹内
1
jupyter notebook --generate-config

  1. 查找该文件中的c.NotebookApp.notebook_dir更改为c.NotebookApp.notebook_dir = 'F:\Jupyter'并保存，此时默认路径就更改为'F:\Jupyter'

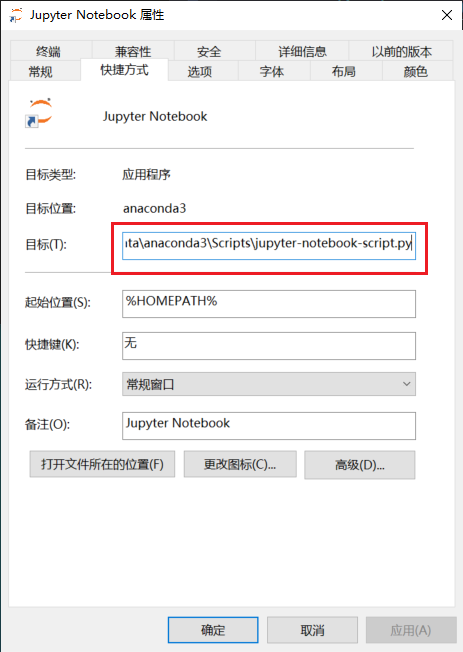
  2. 修改 jupyter 快捷方式的打开方式，删除后面的环境变量，至此修改成功。

将 conda 虚拟环境关联至 jupyter

安装 ipykernel

1
2
conda activate pytorch
pip install ipykernel

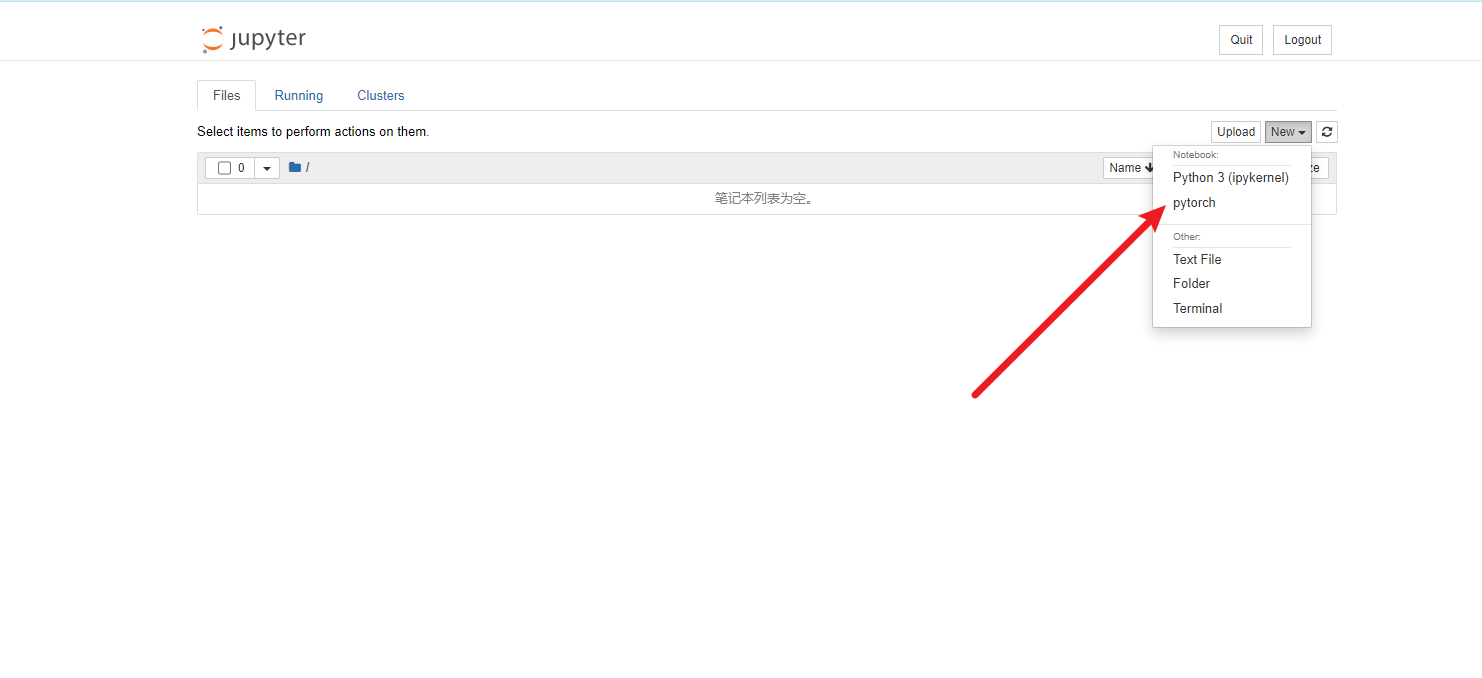
导入

1
python -m ipykernel install --user --name=pytorch

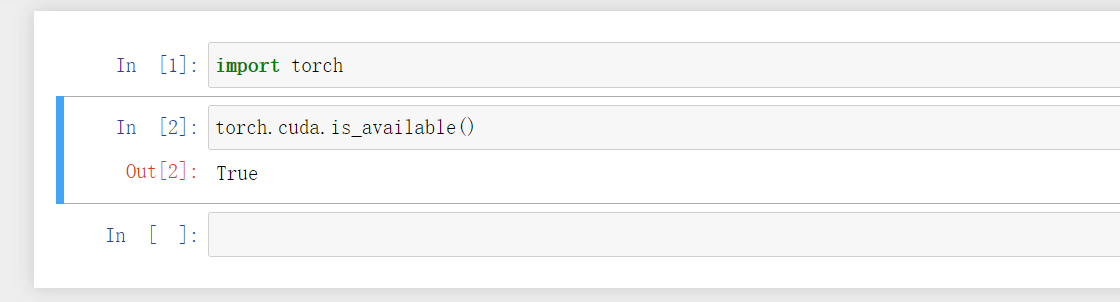
测试 conda 是否可用

2、DNN 基本原理

主要可分为以下 4 个步骤：

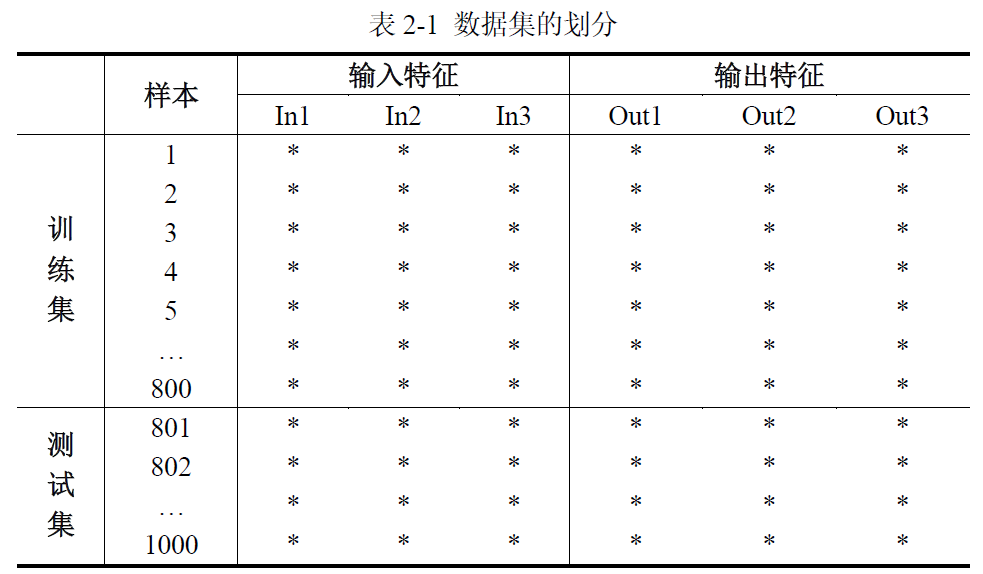
  1. 划分数据集
  2. 训练网络
  3. 测试网络
  4. 使用网络

2.1 划分数据集

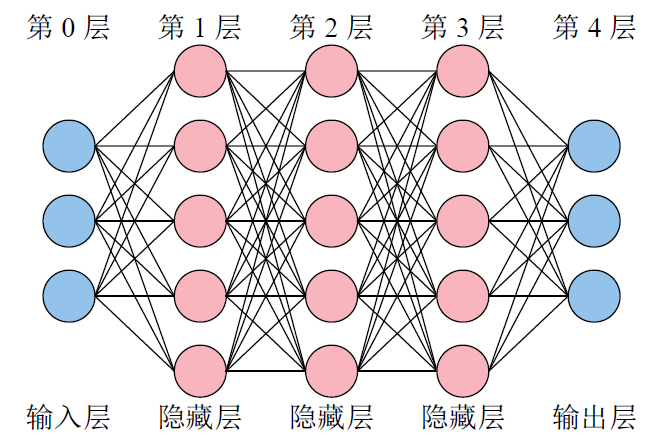
神经网络的结构

考虑到 Python 列表、NumPy 数组以及 PyTorch 张量都是从索引[0]开始，再加之输入层没有内部参数（权重 ω 与偏置 b），所以习惯将输入层称之为第 0 层。

2.2 训练网络

神经网络的训练过程，就是经过很多次前向传播与反向传播的轮回，最终不断调整其内部参数（权重 ω 与偏置 b），以拟合任意复杂函数的过程。内部参数一开始是随机的（如 Xavier 初始值、He 初始值），最终会不断优化到最佳。

习惯把内部参数称为参数，外部参数称为超参数。

（1）前向传播

将单个样本的 3 个输入特征送入神经网络的输入层后，神经网络会逐层计算到输出层，最终得到神经网络预测的 3 个输出特征。

该神经元节点的计算过程为\(y=\omega_1x_1+\omega_2x_2+\omega_3x_3+b\)。你可以理解为，每一根 线就是一个权重 ω，每一个神经元节点也都有它自己的偏置 b。当然，每个神经元节点在计算完后，由于这个方程是线性的，因此必须在外面套一个非线性的函数：\(y=\sigma\left(\omega_1x_1+\omega_2x_2+\omega_3x_3+b\right)\) ，σ 被称为激活函数。如果你不套非线性函数，那么即使 10 层的网络，也可以用 1 层就拟合出同样的方程。

（2）反向传播

经过前向传播，网络会根据当前的内部参数计算出输出特征的预测值。为计算预测值与真实值之间的差距，需要一个损失函数。

损失函数计算好后，逐层退回求梯度。即看每一个内部参数是变大还是变小，才会使得损失函数变小。这样就达到了优化内部参数的目的。

关键参数：外部参数叫学习率。学习率越大，内部参数的优化越快，但过大的学习率可能会使损失函数越过最低点，并在谷底反复横跳。

（3）batch_size

前向传播与反向传播一次时，有三种情况：

  • 批量梯度下降（Batch Gradient Descent，BGD），把所有样本一次性输入进网络，这种方式计算量开销很大，速度也很慢。
  • 随机梯度下降（Stochastic Gradient Descent，SGD），每次只把一个样本输入进网络，每计算一个样本就更新参数。这种方式虽然速度比较快，但是收敛性能差，可能会在最优点附近震荡，两次参数的更新也有可能抵消。
  • 小批量梯度下降（Mini-Batch Gradient Decent，MBGD）是为了中和上面二者而生，这种办法把样本划分为若干个批，按批来更新参数。

PyTorch 只支持批量与小批量

（4）epochs

1 个 epoch 就是指全部样本进行 1 次前向传播与反向传播。

假设有 10240 个训练样本，batch_size 是 1024，epochs 是 5。那么：

  • 全部样本将进行 5 次前向传播与反向传播；
  • 1 个 epoch，将发生 10 次（10240x1024）前向传播与反向传播；
  • 一共发生 50 次（105）前向传播和反向传播。

2.3 测试网络

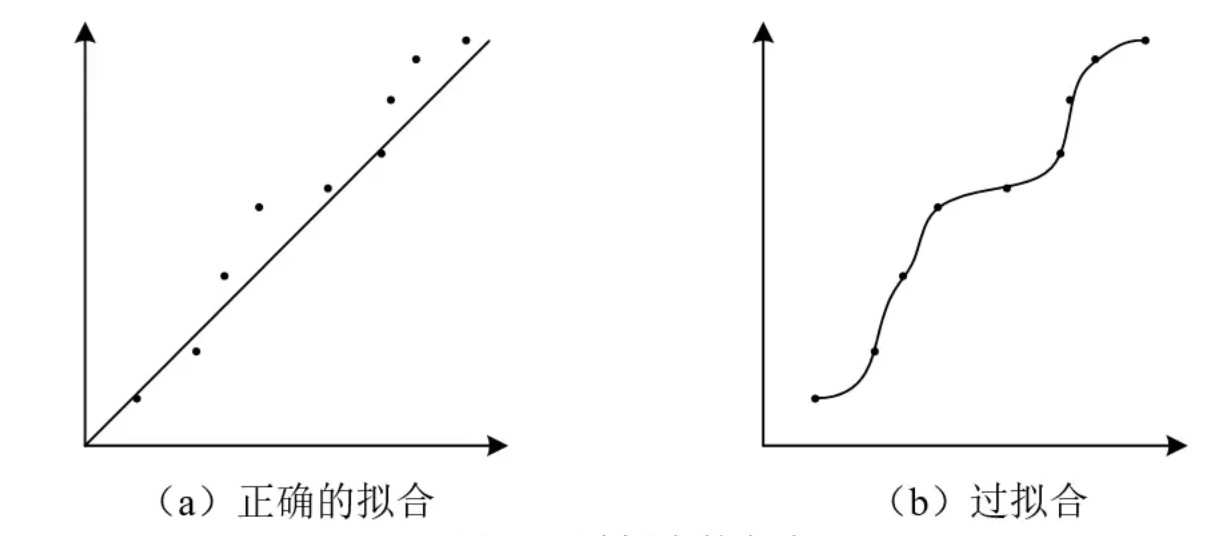
目的：防止过拟合。 过拟合：网络优化好的内部参数支队本训练样本有效。

测试集时，只需要一次前向传播。

2.4 使用网络

直接将样本进行 1 次前向传播。

3、DNN 的实现

3.1 制作数据集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 展示高清图
from matplotlib_inline import backend_inline
backend_inline.set_matplotlib_formats('svg')

X1 = torch.rand(10000,1) # 输入特征1
X2 = torch.rand(10000,1) # 输入特征2
X3 = torch.rand(10000,1) # 输入特征3

Y1 = ( (X1+X2+X3)<1 ).float() # 输出特征1
Y2 = ( (1<(X1+X2+X3)) & ((X1+X2+X3)<2) ).float() # 输出特征2
Y3 = ( (X1+X2+X3)>2 ).float() # 输出特征3
Data = torch.cat([X1,X2,X3,Y1,Y2,Y3],axis=1) # 整合数据集
Data = Data.to('cuda:0') # 把数据集搬到GPU 上

# 划分训练集与测试集
train_size = int(len(Data) * 0.7) # 训练集的样本数量
test_size = len(Data) - train_size # 测试集的样本数量
Data = Data[torch.randperm( Data.size(0)) , : ] # 打乱样本的顺序
train_Data = Data[ : train_size , : ] # 训练集样本
test_Data = Data[ train_size : , : ] # 测试集样本
train_Data.shape, test_Data.shape

3.2 搭建神经网络

通常以 nn.Module 作为父类，自己的神经网络可直接继承父类的方法和属性。

在定义神经网络时通常需要包含 2 个方法，__init__和forward

  • __init__：用于构建自己的神经网络
  • forward：用于输入数据进行向前传播

（1）搭建神经网络结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class DNN(nn.Module):
    def __init__(self):
        ''' 搭建神经网络各层 '''
        super(DNN,self).__init__()
        self.net = nn.Sequential( # 按顺序搭建各层
            nn.Linear(3, 5), nn.ReLU(), # 第1 层：全连接层
            nn.Linear(5, 5), nn.ReLU(), # 第2 层：全连接层
            nn.Linear(5, 5), nn.ReLU(), # 第3 层：全连接层
            nn.Linear(5, 3) # 第4 层：全连接层
        )
    def forward(self, x):
        ''' 前向传播 '''
        y = self.net(x) # x 即输入数据
        return y # y 即输出数据

代码解析

1
nn.Linear(3, 5), nn.ReLU()
  • 表示一个隐藏层，第一个隐藏层为线性层，搜嘎会给你一个神经元节点数是 3，这层节点数是 5
  • 后面的nn.ReLU()表示一个激活函数

代码解析

1
2
3
4
nn.Linear(3, 5), nn.ReLU(), # 第1 层：全连接层
nn.Linear(5, 5), nn.ReLU(), # 第2 层：全连接层
nn.Linear(5, 5), nn.ReLU(), # 第3 层：全连接层
nn.Linear(5, 3) # 第4 层：全连接层

第二层的第一个数要和第一层的第二个数对应

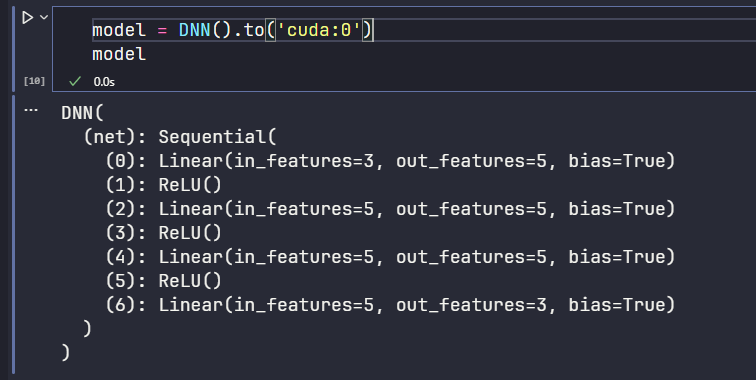
（2）创建神经网络

创建 model 实例，并将其转移掉 gpu 上

  • 每个隐藏层都有一个激活函数。
  • 各层的神经元节点数位 3 5 5 5 3

输入层的神经元数量必须与每个样本的输入特征数量一致，输出层的神经数量必须与每个样本的输出特征数量一致。

3.3 网络的内部参数

权重与偏置

查看网络内部参数

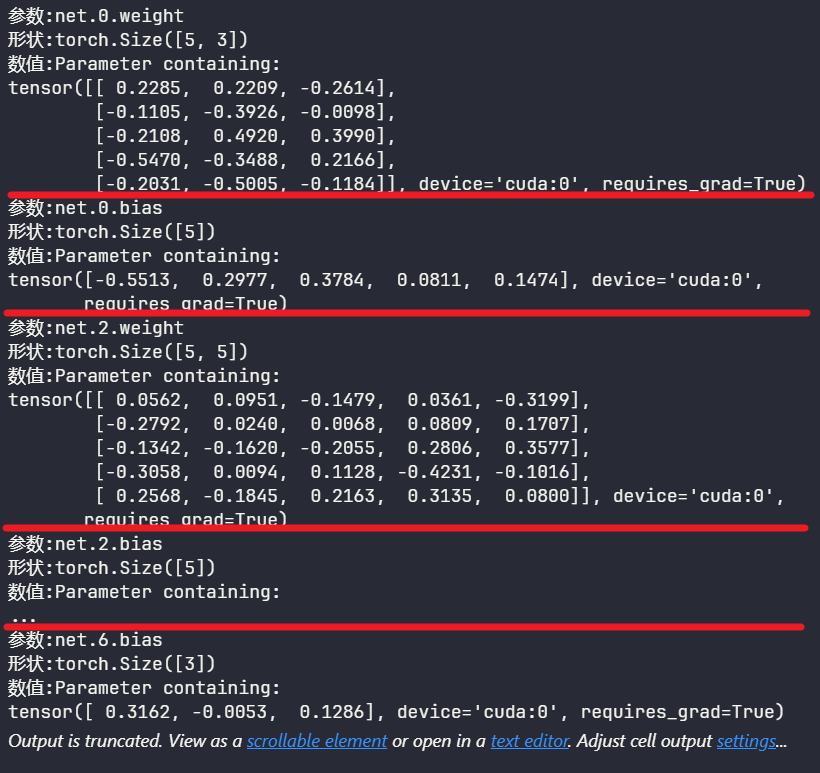
1
2
for name,param in model.named_parameters():
    print(f"参数:{name}\n形状:{param.shape}\n数值:{param}")

  • net.0.weight 权重形状为[5,3]，5 表示自己的节点数，3 表示前一层的节点数
  • device='cuda:0'表示在 gpu 上
  • requires_grad=True表示打开梯度计算功能

3.4 网络外部参数

又叫超参数。

  • 搭建网络时的超参数：网络的层数、各隐藏层节点数、各节点激活函数、内部参数的初始值等。
  • 训练网络时的超参数：损失函数、学习率、优化算法、batch_size、epochs 等。

（1）激活函数

引入非线性因素，从而使神经网络能够学习和表达更加复杂的函数关系。

官网

https://cloud.tencent.com/developer/article/1797190

（2）损失函数

计算神经网络每次迭代的前向计算结果与真实值的差距，从而指导下一步的训练向正确的方向进行。

官网

1
2
3
4
5
6
# 损失函数的选择
loss_fn = nn.MSELoss()

# 优化算法的选择
learning_rate = 0.01 # 设置学习率
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

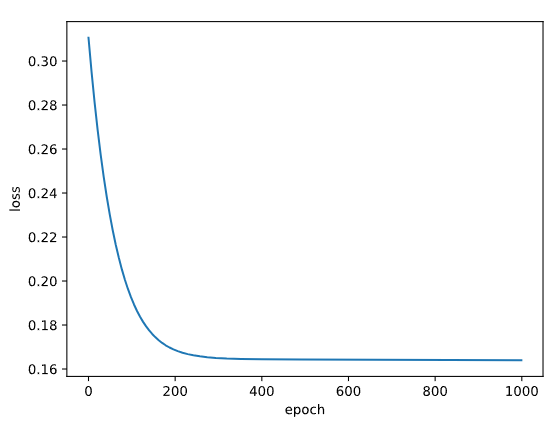
3.5 训练网路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 训练网络
epochs = 1000
losses = [] # 记录损失函数变化的列表
# 给训练集划分输入与输出
X = train_Data[ : , :3 ] # 前3 列为输入特征
Y = train_Data[ : , -3: ] # 后3 列为输出特征
for epoch in range(epochs):
    Pred = model(X) # 一次前向传播（批量）
    loss = loss_fn(Pred, Y) # 计算损失函数
    losses.append(loss.item()) # 记录损失函数的变化
    optimizer.zero_grad() # 清理上一轮滞留的梯度
    loss.backward() # 一次反向传播
    optimizer.step() # 优化内部参数
Fig = plt.figure()
plt.plot(range(epochs), losses)
plt.ylabel('loss'), plt.xlabel('epoch')
plt.show()

3.6 测试神网络

1
2
3
4
5
6
7
8
9
10
11
# 测试网络
# 给测试集划分输入与输出
X = test_Data[:, :3] # 前3 列为输入特征
Y = test_Data[:, -3:] # 后3 列为输出特征
with torch.no_grad(): # 该局部关闭梯度计算功能
    Pred = model(X) # 一次前向传播（批量）
    Pred[:,torch.argmax(Pred, axis=1)] = 1
    Pred[Pred!=1] = 0
    correct = torch.sum( (Pred == Y).all(1) ) # 预测正确的样本
    total = Y.size(0) # 全部的样本数量
    print(f'测试集精准度: {100*correct/total} %')

3.7 保存与导入网络

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 保存网络
torch.save(model,'model.pth')

# 导入网络
new_model =torch.load('model.pth')

# 测试新网络
# 给测试集划分输入与输出
X = test_Data[:, :3] # 前3 列为输入特征
Y = test_Data[:, -3:] # 后3 列为输出特征
with torch.no_grad(): # 该局部关闭梯度计算功能
    Pred = new_model(X) # 用新模型进行一次前向传播
    Pred[:,torch.argmax(Pred, axis=1)] = 1
    Pred[Pred!=1] = 0
    correct = torch.sum( (Pred == Y).all(1) ) # 预测正确的样本
    total = Y.size(0) # 全部的样本数量
    print(f'测试集精准度: {100*correct/total} %')

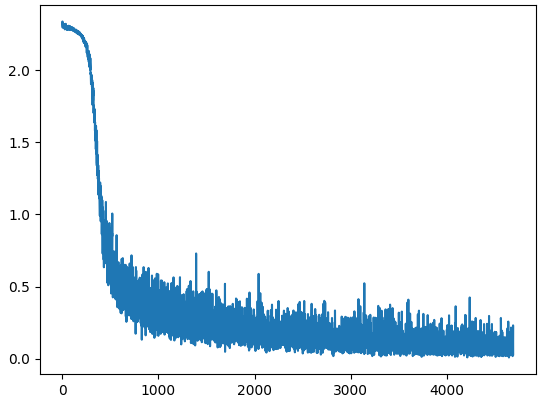
4、批量梯度下降案例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 展示高清图
from matplotlib_inline import backend_inline
backend_inline.set_matplotlib_formats('svg')

# 准备数据集
df = pd.read_csv('Data.csv', index_col=0) # 导入数据
arr = df.values # Pandas 对象退化为NumPy 数组
arr = arr.astype(np.float32) # 转为float32 类型数组
ts = torch.tensor(arr) # 数组转为张量
ts = ts.to('cuda') # 把训练集搬到cuda 上

# 划分训练集与测试集
train_size = int(len(ts) * 0.7) # 训练集的样本数量
test_size = len(ts) - train_size # 测试集的样本数量
ts = ts[ torch.randperm( ts.size(0) ) , : ] # 打乱样本的顺序
train_Data = ts[ : train_size , : ] # 训练集样本
test_Data = ts[ train_size : , : ] # 测试集样本

# 创建神经网络
class DNN(nn.Module):
    def __init__(self):
        ''' 搭建神经网络各层 '''
        super(DNN,self).__init__()
        self.net = nn.Sequential( # 按顺序搭建各层
        nn.Linear(8, 32), nn.Sigmoid(), # 第1 层：全连接层
        nn.Linear(32, 8), nn.Sigmoid(), # 第2 层：全连接层
        nn.Linear(8, 4), nn.Sigmoid(), # 第3 层：全连接层
        nn.Linear(4, 1), nn.Sigmoid() # 第4 层：全连接层
        )
    def forward(self, x):
        ''' 前向传播 '''
        y = self.net(x) # x 即输入数据
        return y # y 即输出数据

model = DNN().to('cuda:0') # 创建子类的实例，并搬到GPU 上

# 损失函数的选择
loss_fn = nn.BCELoss(reduction='mean')

# 优化算法的选择
learning_rate = 0.005 # 设置学习率
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

# 训练网络
epochs = 5000
losses = [] # 记录损失函数变化的列表
# 给训练集划分输入与输出
X = train_Data[ : , : -1 ] # 前8 列为输入特征
Y = train_Data[ : , -1 ].reshape((-1,1)) # 后1 列为输出特征
# 此处的.reshape((-1,1))将一阶张量升级为二阶张量
for epoch in range(epochs):
    Pred = model(X) # 一次前向传播（批量）
    loss = loss_fn(Pred, Y) # 计算损失函数
    losses.append(loss.item()) # 记录损失函数的变化
    optimizer.zero_grad() # 清理上一轮滞留的梯度
    loss.backward() # 一次反向传播
    optimizer.step() # 优化内部参数
Fig = plt.figure()
plt.plot(range(epochs), losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

# 测试网络
# 给测试集划分输入与输出
X = test_Data[ : , : -1 ] # 前8 列为输入特征
Y = test_Data[ : , -1 ].reshape((-1,1)) # 后1 列为输出特征
with torch.no_grad(): # 该局部关闭梯度计算功能
    Pred = model(X) # 一次前向传播（批量）
    Pred[Pred>=0.5] = 1
    Pred[Pred<0.5] = 0
    correct = torch.sum( (Pred == Y).all(1) ) # 预测正确的样本
    total = Y.size(0) # 全部的样本数量
    print(f'测试集精准度: {100*correct/total} %')

5、小批量梯度下降

在使用小批量梯度下降时，必须使用 3 个 PyTorch 内置的实用工具（utils）：

  • DataSet 用于封装数据集；
  • DataLoader 用于加载数据不同的批次；
  • random_split 用于划分训练集与测试集
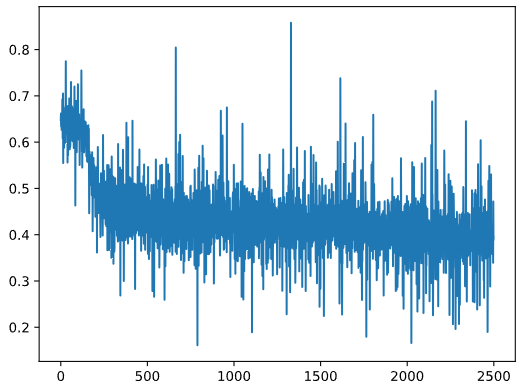
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from torch.utils.data import random_split
import matplotlib.pyplot as plt
%matplotlib inline

# 展示高清图
from matplotlib_inline import backend_inline
backend_inline.set_matplotlib_formats('svg')

# 制作数据集
class MyData(Dataset): # 继承Dataset 类
    def __init__(self, filepath):
        df = pd.read_csv(filepath, index_col=0) # 导入数据
        arr = df.values # 对象退化为数组
        arr = arr.astype(np.float32) # 转为float32 类型数组
        ts = torch.tensor(arr) # 数组转为张量
        ts = ts.to('cuda') # 把训练集搬到cuda 上
        self.X = ts[ : , : -1 ] # 前8 列为输入特征
        self.Y = ts[ : , -1 ].reshape((-1,1)) # 后1 列为输出特征
        self.len = ts.shape[0] # 样本的总数
    def __getitem__(self, index):
        return self.X[index], self.Y[index]
    def __len__(self):
        return self.len

# 划分训练集与测试集
Data = MyData('Data.csv')
train_size = int(len(Data) * 0.7) # 训练集的样本数量
test_size = len(Data) - train_size # 测试集的样本数量
train_Data, test_Data = random_split(Data, [train_size, test_size])

# 批次加载器
train_loader = DataLoader(dataset=train_Data, shuffle=True, batch_size=128) # shuffle洗牌
test_loader = DataLoader(dataset=test_Data, shuffle=False, batch_size=64) # 测试集就不需要洗牌了

# 搭建神经网络
class DNN(nn.Module):
    def __init__(self):
        ''' 搭建神经网络各层 '''
        super(DNN,self).__init__()
        self.net = nn.Sequential( # 按顺序搭建各层
        nn.Linear(8, 32), nn.Sigmoid(), # 第1 层：全连接层
        nn.Linear(32, 8), nn.Sigmoid(), # 第2 层：全连接层
        nn.Linear(8, 4), nn.Sigmoid(), # 第3 层：全连接层
        nn.Linear(4, 1), nn.Sigmoid() # 第4 层：全连接层
        )
    def forward(self, x):
        ''' 前向传播 '''
        y = self.net(x) # x 即输入数据
        return y # y 即输出数据

model = DNN().to('cuda:0') # 创建子类的实例，并搬到GPU 上
model # 查看该实例的各层

# 优化算法的选择
learning_rate = 0.005 # 设置学习率
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

# 训练网络
epochs = 500
losses = [] # 记录损失函数变化的列表
for epoch in range(epochs):
    for (x, y) in train_loader: # 获取小批次的x 与y
        Pred = model(x) # 一次前向传播（小批量）
        loss = loss_fn(Pred, y) # 计算损失函数
        losses.append(loss.item()) # 记录损失函数的变化
        optimizer.zero_grad() # 清理上一轮滞留的梯度
        loss.backward() # 一次反向传播
        optimizer.step() # 优化内部参数
Fig = plt.figure()
plt.plot(range(len(losses)), losses)
plt.show()

# 测试网络
correct = 0
total = 0
with torch.no_grad(): # 该局部关闭梯度计算功能
    for (x, y) in test_loader: # 获取小批次的x 与y
        Pred = model(x) # 一次前向传播（小批量）
        Pred[Pred>=0.5] = 1
        Pred[Pred<0.5] = 0
        correct += torch.sum( (Pred == y).all(1) )
        total += y.size(0)
print(f'测试集精准度: {100*correct/total} %')

小批量时针对局部进行向前向后，所以出来的损失函数不是梯度下降的。

6、手写数字识别

手写数字识别数据集（MNIST）是机器学习领域的标准数据集

  • 输入：一副图像
  • 输出：一个与图像中对应的数字（0 至 9 之间的一个整数，不是独热编码）

我们不用手动将输出转换为独热编码，PyTorch 会在整个过程中自动将数据集的输出转换为独热编码.只有在最后测试网络时，我们对比测试集的预测输出与真实输出时，才需要注意一下。

1
2
3
4
5
6
7
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
from torchvision import transforms # 需要使用pip install安装一下
from torchvision import datasets
import matplotlib.pyplot as plt
%matplotlib inline

下载时需要开启全局代理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
# 制作数据集
# 数据集转换参数
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize(0.1307, 0.3081)
])

# 下载训练集与测试集
train_Data = datasets.MNIST(
    root = 'F:\Jupyter\pytorch\dataset\mnist', # 下载路径
    train = True, # 是train 集
    download = True, # 如果该路径没有该数据集，就下载
    transform = transform # 数据集转换参数
)

test_Data = datasets.MNIST(
    root = 'F:\Jupyter\pytorch\dataset\mnist', # 下载路径
    train = False, # 是test 集
    download = True, # 如果该路径没有该数据集，就下载
    transform = transform # 数据集转换参数
)

# 批次加载器
train_loader = DataLoader(train_Data, shuffle=True, batch_size=64)
test_loader = DataLoader(test_Data, shuffle=False, batch_size=64)

'''
每个样本的输入都是形状为2828的二维数组，那么对于 DNN 来说，输入层的神经元节点就要有28x28 = 784个；输出层使用独热编码，需要 10 个节点。
'''
class DNN(nn.Module):
    def __init__(self):
        ''' 搭建神经网络各层 '''
        super(DNN,self).__init__()
        self.net = nn.Sequential( # 按顺序搭建各层
        nn.Flatten(), # 把图像铺平成一维
        nn.Linear(784, 512), nn.ReLU(), # 第1 层：全连接层
        nn.Linear(512, 256), nn.ReLU(), # 第2 层：全连接层
        nn.Linear(256, 128), nn.ReLU(), # 第3 层：全连接层
        nn.Linear(128, 64), nn.ReLU(), # 第4 层：全连接层
        nn.Linear(64, 10) # 第5 层：全连接层
    )
    def forward(self, x):
        ''' 前向传播 '''
        y = self.net(x) # x 即输入数据
        return y # y 即输出数据

model = DNN().to('cuda:0') # 创建子类的实例，并搬到GPU 上
model # 查看该实例的各层

# 损失函数的选择
loss_fn = nn.CrossEntropyLoss() # 自带softmax 激活函数

# 优化算法的选择
learning_rate = 0.01 # 设置学习率
optimizer = torch.optim.SGD(
    model.parameters(),
    lr = learning_rate,
    momentum = 0.5
)

# 训练网络
epochs = 5
losses = [] # 记录损失函数变化的列表
for epoch in range(epochs):
    for (x, y) in train_loader: # 获取小批次的x 与y
        x, y = x.to('cuda:0'), y.to('cuda:0')
        Pred = model(x) # 一次前向传播（小批量）
        loss = loss_fn(Pred, y) # 计算损失函数
        losses.append(loss.item()) # 记录损失函数的变化
        optimizer.zero_grad() # 清理上一轮滞留的梯度
        loss.backward() # 一次反向传播
        optimizer.step() # 优化内部参数
Fig = plt.figure()
plt.plot(range(len(losses)), losses)
plt.show()

# 测试网络
correct = 0
total = 0
with torch.no_grad(): # 该局部关闭梯度计算功能
    for (x, y) in test_loader: # 获取小批次的x 与y
        x, y = x.to('cuda:0'), y.to('cuda:0')
        Pred = model(x) # 一次前向传播（小批量）
        _, predicted = torch.max(Pred.data, dim=1)
        correct += torch.sum( (predicted == y) )
        total += y.size(0)
print(f'测试集精准度: {100*correct/total} %')

测试集精准度: 97.06999969482422 %

编程 > 大模型
#编程 #学习笔记 #python #深度学习 #pytorch
深度学习入门
http://example.com/2024/06/30/028 深度学习入门/
作者
DB
发布于
2024年6月30日
许可协议