The Spalart-Allmaras Turbulence Model
1、历史发展
流体动力学中描述流体在外力作用下流动的主要控制方程是纳维-斯托克斯方程。这些方程的强大之处在于它们能够描述作用在流体上的任何力的影响以及由此产生的流动行为。然而,它们不能针对每个系统或流量情况以封闭形式求解。
由于最早 1973 年提出的 ke 模型无法准确预测逆压力梯度 adverse pressure gradient 下的边界层运动,Spalart-Allmaras Model(1994)、(1998)以及 (1994)分别被提出。
在物理学中,Spalart-Allmaras 模型是一种单方程模型,可求解运动涡流湍流粘度的模拟输运方程。在其原始形式中,该模型实际上是一个低雷诺数模型,需要正确解析边界层的粘度影响区域(y+ ~1 个网格)。它没有针对一般工业流动进行标定,对于一些自由剪切流,尤其是平面和圆形射流,确实会产生较大的误差。此外,不能依靠它来预测均匀、各向同性湍流的衰减。
2、基本形式
\[\tau_{ij}=2\mu_t\left(S_{ij}-\frac{1}{3}\frac{\partial u_k}{\partial x_k}\delta_{ij}\right)-\frac{2}{3}\rho k\delta_{ij}\]
Spalart-Allmaras 湍流模型遵循一个描述运动粘度类变量(称为 Spalart-Allmaras 变量)的动态方程:
\[\frac{\partial\bar{v}}{\partial t}+u_{j}\frac{\partial\bar{v}}{\partial x_{j}}=C_{b,1}(1-f_{t,2})\hat{S}\bar{v}-[c_{w,1}f_{w}-\frac{c_{b,1}}{\kappa^{2}}f_{t,2}](\frac{\bar{v}}{d})^{2}+\frac{1}{\sigma}[\frac{\partial}{\partial x_{j}}((v+\bar{v})\frac{\partial\bar{v}}{\partial x_{j}})+c_{b,2}\frac{\partial\bar{v}}{\partial x_{i}}\frac{\partial\bar{v}}{\partial x_{i}}]\]
该方程的目标是确定湍流涡流粘度,其由以下公式确定:
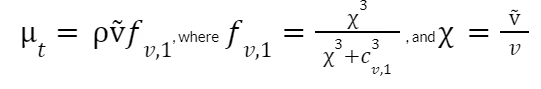
在这些方程中,分子运动粘度为 𝜈 = μ/⍴,流体密度为 ⍴,μ 是流体的分子动力粘度。模型中的其他参数以场点到最近壁 d 的距离和涡度大小给出
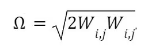
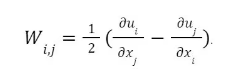
以下定义:
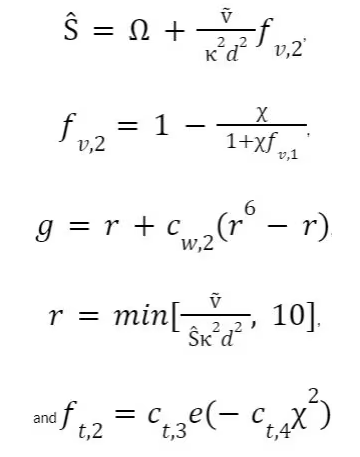
从上面的定义中可以看出几个常量。这些常量定义如下:
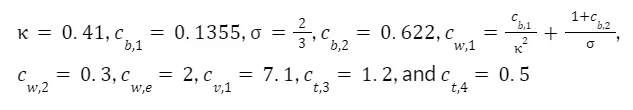
由于所考虑的系统以墙为界,因此沿着墙的表面有一个固定边界条件。其他边界条件可能会施加在系统的其他地方,尽管这些边界条件是否会干扰解决远离壁本身的涡流可能值得怀疑。最后,我们对远场 Spalart-Allmaras 变量有以下条件:
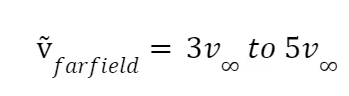
优点:
- 降维可以降低问题的复杂性和整体模拟时间。
- 无需使用沿湍流的剪切层的局部厚度来计算长度尺度。
- 对于具有任意压力梯度的边界层流很有用。
- 稳健;对于低雷诺数 k - ε 模型不收敛甚至发散的相对粗糙的网格,它可以给出合理的结果
缺点:
- 不适用于涉及喷射状自由剪切区域的应用
3、用途
4、注意事项
参考:
- https://resources.system-analysis.cadence.com/blog/msa2024-what-is-the-spalart-allmaras-turbulence-model
- https://www.cfd-online.com/Wiki/Spalart-Allmaras_model
- https://www.youtube.com/watch?v=Xivc0EIGFQw
- https://zhuanlan.zhihu.com/p/408434524