深度学习基础

本文最新更新于 2025/02/08 晚上

梯度下降 线性回归 学习率

---

Github资料

1、机器学习分类

分为监督学习和无监督学习

1.1 监督学习

• 定义：在给定的数据集中学习出一个函数，当输入新的x时，能够预测输出结果y。
• 两种主要类型：回归和分类
• 学习技术：逻辑回归、线性回归、决策树和神经网络。

1.2 无监督学习

• 无监督学习算法会使用未标记的数据进行训练。
• 无监督学习可用于将新闻文章分类
• 学习技术：集群、关联规则学习、概率密度和降维

1.3 区别

• 监督学习是一种目的明确的训练方式，你知道得到的是什么；而无监督学习则是没有明确目的的训练方式，你无法提前知道结果是什么。
• 监督学习由于目标明确，所以可以衡量效果；而无监督学习几乎无法量化效果如何。

1. 有监督学习和无监督学习有什么区别
2. 无监督学习 – Unsupervised learning | UL

2、线性回归

2.1 定义

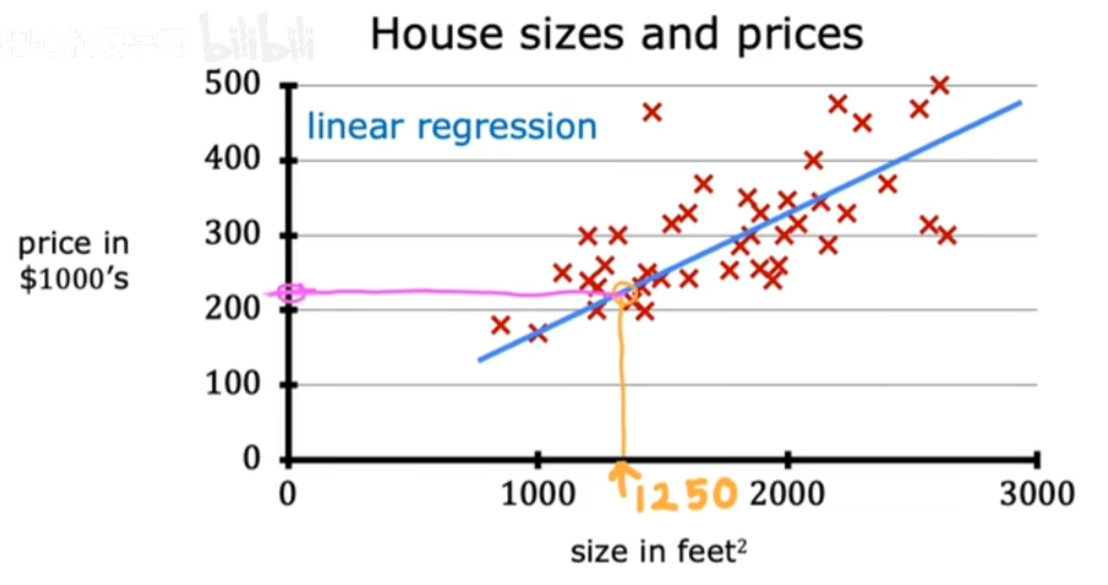
任何预测数字之间的监督学习模型都可被称作回归问题。线性回归时回归模型中的一个用例。 模型可以有无限可能的输出。

Training : Data used to train the model

• x : 输入
• y : 输出
• m : 训练集的数量
• (x,y) : 单个训练样本
• $ (x^{i},y{i}) $ : 第i个训练样本fs
• \(\hat{y}\) : 预测值
• f : 函数模型
• \(\hat{y}-y\) : error

另一种机器学习类别是分类，分类问题时预测类别或者离散类别，如预测图片是猫还是狗。 在分类问题中，只有少量可能的输出。

2.2 损失函数

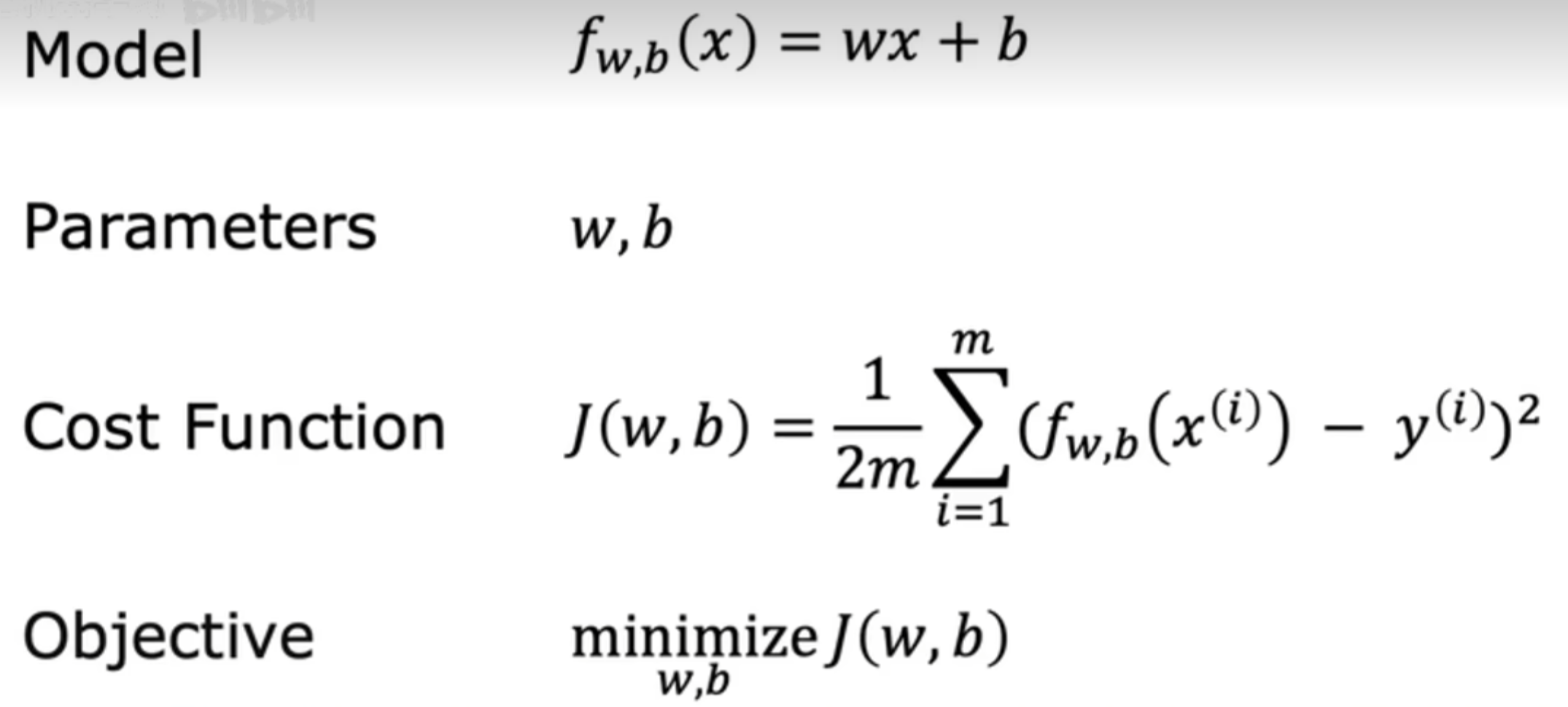
模型 \[ f_{w,b}(x)=wx+b \] 参数为w和b \[ J(w,b)=\frac{1}{2m}\sum_{i=1}^{m}\bigl(f_{w,b}\bigl(x^{(i)}\bigr)-y^{(i)}\bigr)^{2} \]

\(J(w,b)\)最小化

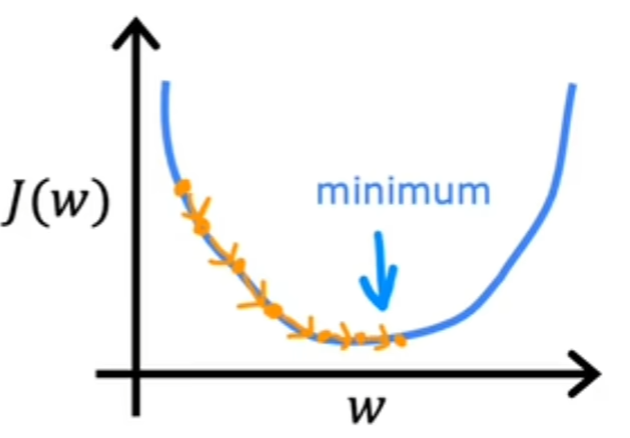
为方便举例，假设只有一个参数w。如图所示，当参数w为1时，J(w)时是最小的

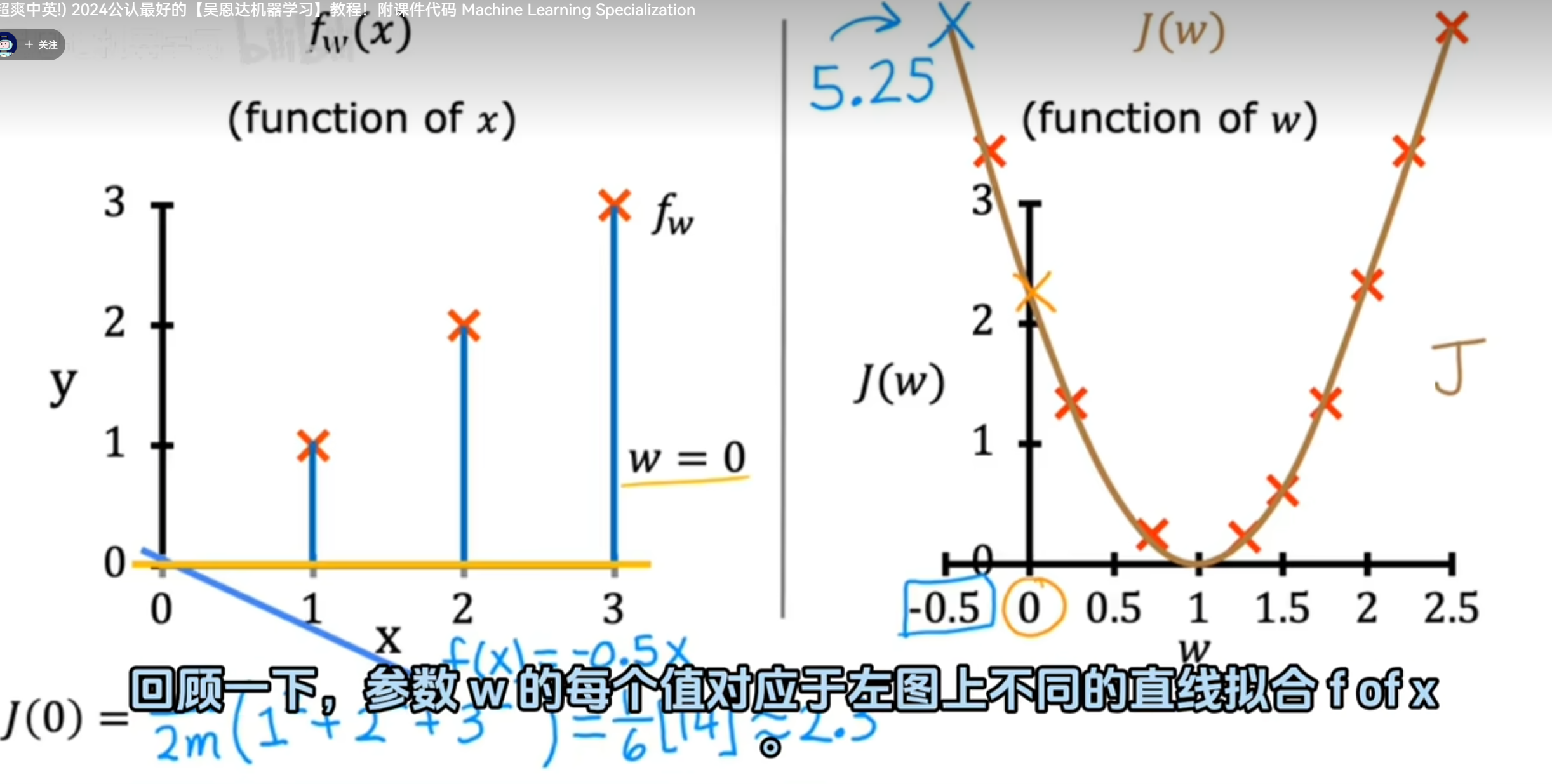
如果参数有w和b则

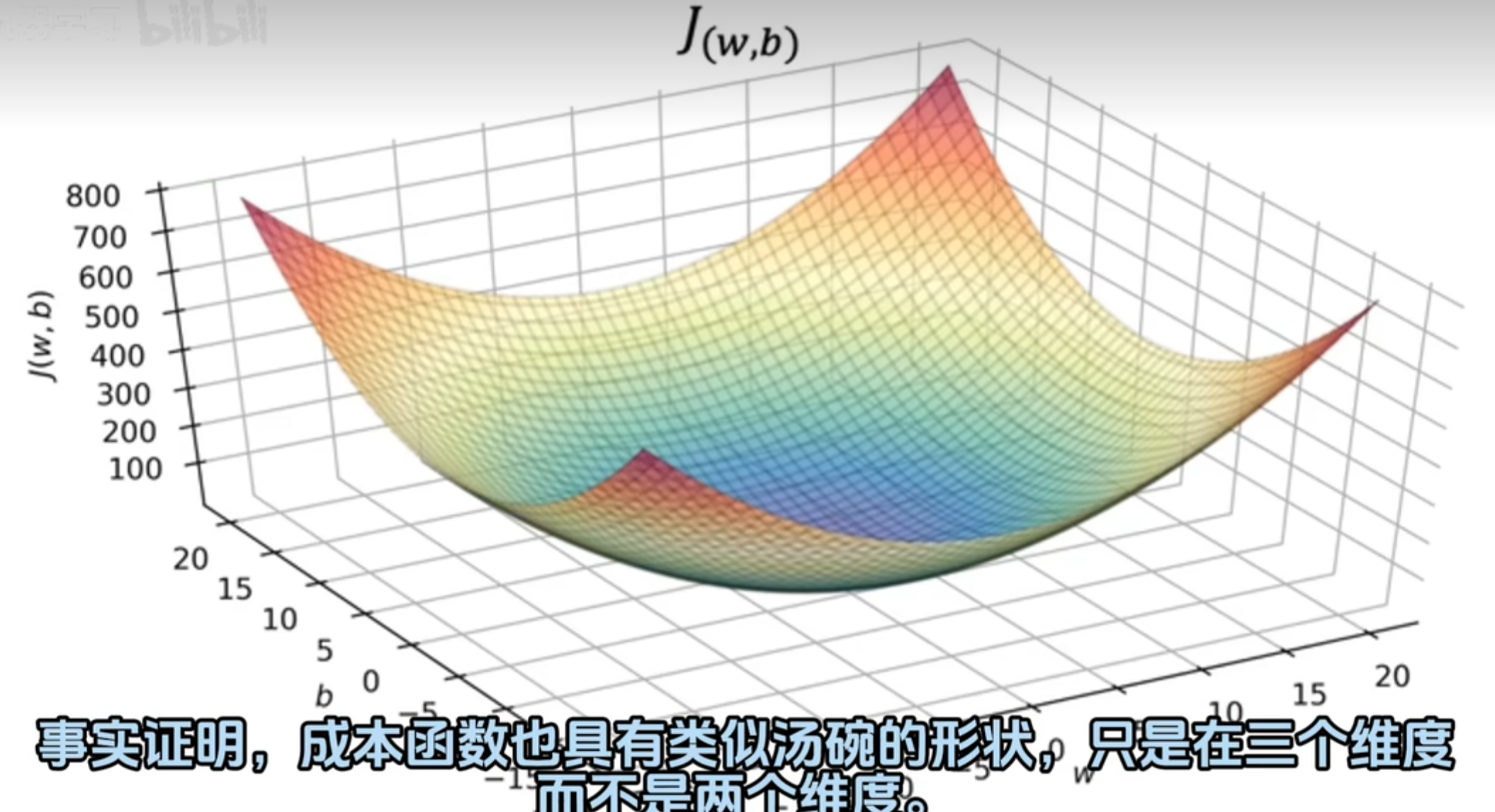
或者

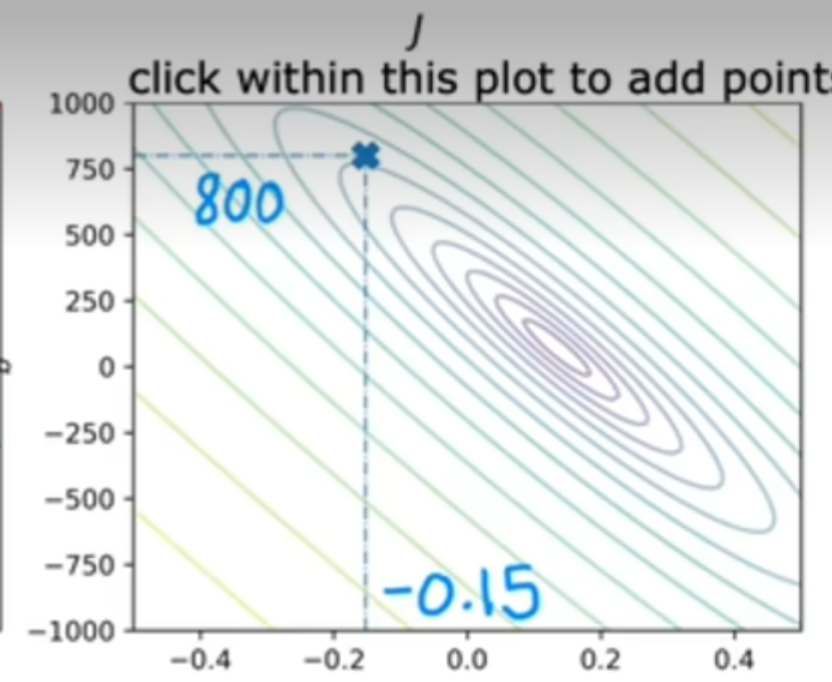
完整对应关系

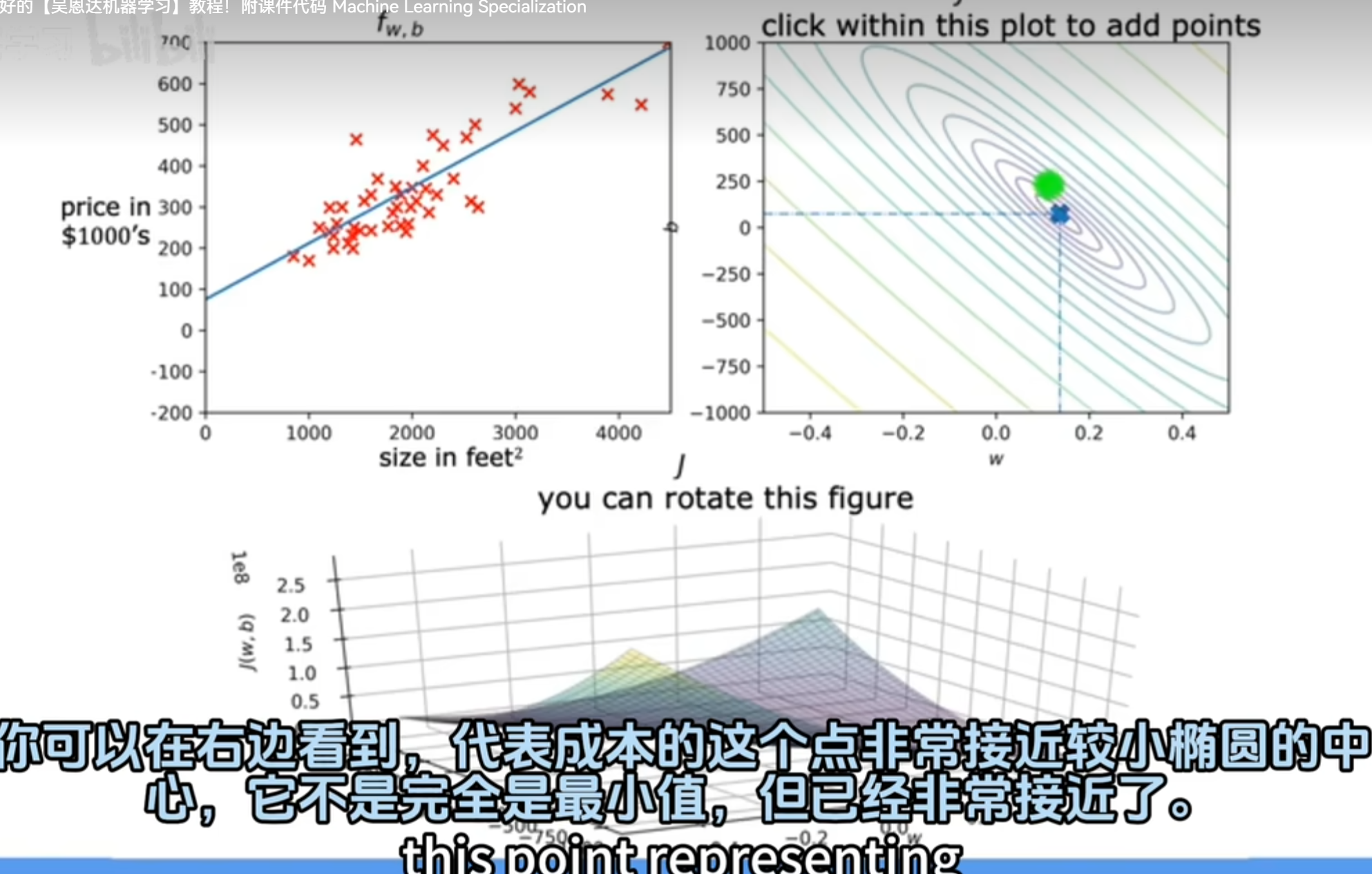
3、梯度下降

有时我们的损失值J并不是规则的，如图所示，存在诸多小峰和低谷。机器学习的目标就是找到最低点，如何快速找到最低点至关重要。

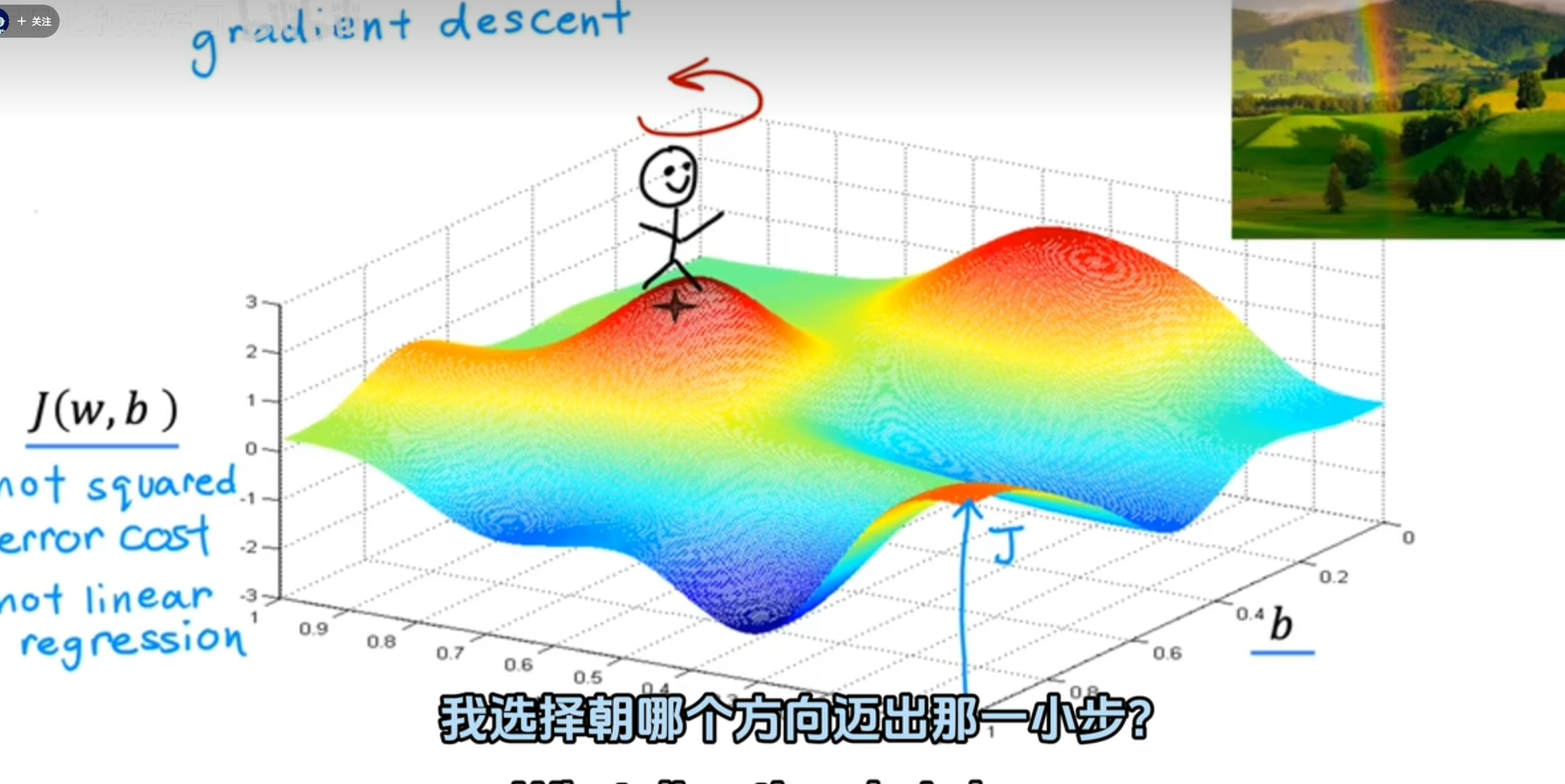
假设你站在一个山坡上，如何找到最快的下坡路线？即朝哪个方向迈出一步？每走一步都要再次确认下一步往哪迈。

实现梯度下降

\[ w=w-\alpha\frac\partial{\partial w}J(w,b) \]

\[ b=b-\alpha\frac\partial{\partial b}J(w,b) \]

学习率\(\alpha\)决定下坡的步数大小

对于某个特定步的两个量(w,b)的更新，\(\frac\partial{\partial w}J(w,b)\)要一致。

\[ tmp_w = w-\alpha\frac\partial{\partial w}J(w,b) \]

\[ tmp_b = b-\alpha\frac\partial{\partial b}J(w,b) \]

\[ w = tmp_w \]

\[ b = tmp_b \]

直观理解梯度下降

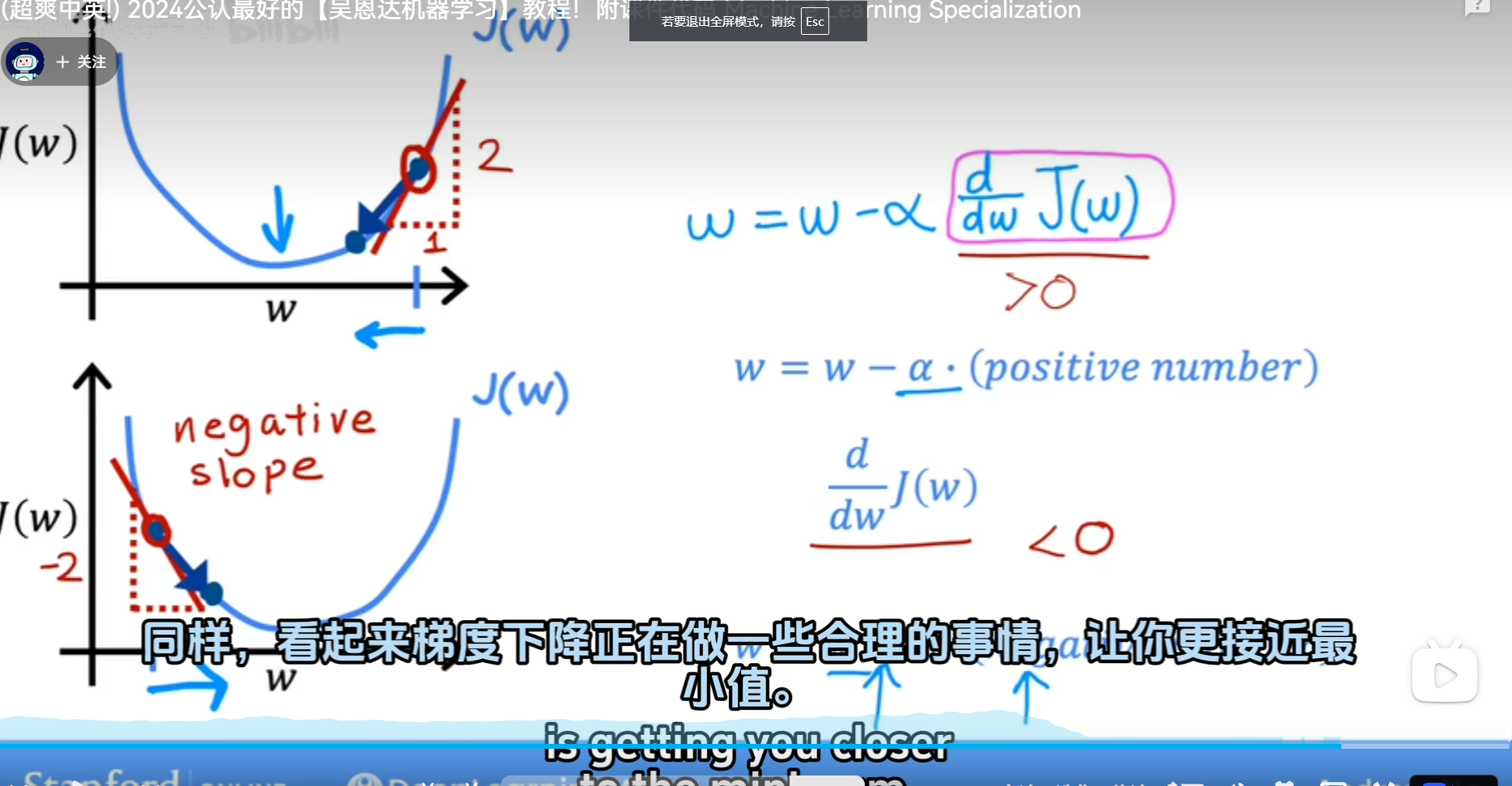
3.1 学习率

学习率的值至关重要，太小和太大会产生什么影响呢？

• 太小学习很慢
• 太大可能会离最小值越来越远，导致发散

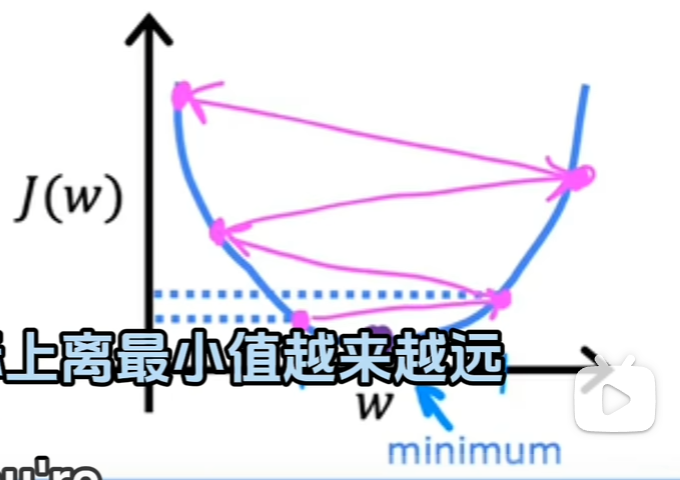
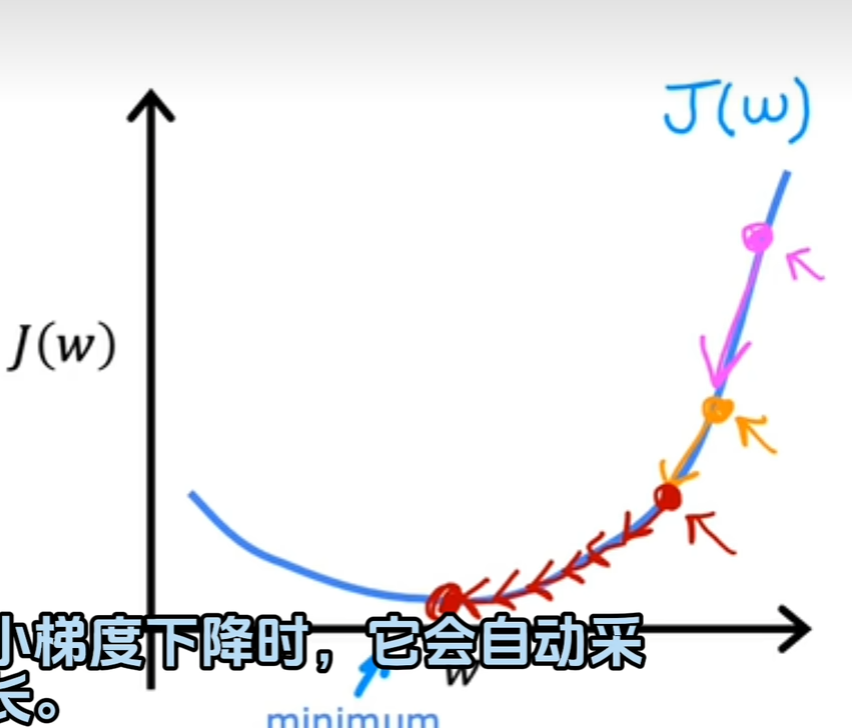
固定的学习率，下降的步长会越来越小，因为导数在变小

3.2 线性回归中的梯度下降

\[ f_{w,b}(x)=wx+b \]

\[ J(w,b)=\frac{1}{2m}\sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})^{2}\]

\[ w=w-\alpha\frac{\partial}{\partial w}J(w,b) \]

\[ b=b-\alpha\frac{\partial}{\partial b}J(w,b) \]

而

\[ \frac{\partial}{\partial w}J(w,b) = \frac{1}{m}\sum_{i=1}^{m}(f_{w,b}\big(x^{(i)}\big)-y^{(i)})x^{(i)} \]

\[ \frac{\partial}{\partial w}J(w,b) = \frac{1}{m}\sum_{i=1}^{m}(f_{w,b}\big(x^{(i)}\big)-y^{(i)}) \]

则

\[ w=w-\alpha\frac{1}{m}\sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)}) x^{(i)} \]

\[ b=b-\alpha\frac{1}{m}\sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)}) \]

梯度下降只能找到局部最小值，而不能找到全局最小值。对于凸函数只有一个最小值，梯度下降是适用的

4、多元线性回归

多元线性回归模型中有多个特征值。比如房间的价格Y不止与面积X1有关，还与地段X2、房间数X3等有关。此时的X实际为一个向量 [X1,X2,X3]。此时模型可以定义为

\[ f_{\overrightarrow{w},b}(\overrightarrow{X})=w_{1}X_{1}+w_{2}X_{2}+w_{3}X_{3}+b \]

\[ \overrightarrow{w} = [X1,X2,X3] \]

\[ f_{\overrightarrow{w},b}(\overrightarrow{X})=\overrightarrow{w}\cdot\overrightarrow{X} + b \]

向量化

\[f=w[0]*x[0]+w[1]*x[1]+w[2]*x[2]+b\] 代码表示

f = 0
for j in range(0,n):
  f = f + w[j] * x[j]
f = f + b

// 也可以使用numpy，这种方式计算效率高，因为numpy可以并行计算
f = np.dot(w,x) + b

向量中的梯度算法

视频讲解

多个特征值

\[ \begin{align*} \text{repeat}&\text{ until convergence:} \; \lbrace \newline\; & w_j = w_j -  \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{5}  \; & \text{for j = 0..n-1}\newline &b\ \ = b -  \alpha \frac{\partial J(\mathbf{w},b)}{\partial b}  \newline \rbrace \end{align*} \]

\[ \frac{\partial J(\mathbf{w},b)}{\partial w_j}=\frac{1}{m}\sum_{i=0}^{m-1}(f_{\mathbf{w},b}(\mathbf{x}^{(i)})-y^{(i)})x_j^{(i)} \]

\[ \frac{\partial J(\mathbf{w},b)}{\partial b}=\frac{1}{m}\sum_{i=0}^{m-1}(f_{\mathbf{w},b}(\mathbf{x}^{(i)})-y^{(i)}) \]

4.1 梯度下降:特征放缩

如果两个特征值在量级上相差较大，如房间数和面积，房间数一般在1_{5，而面积在100}150，这时绘制出的w1和w2的J(w,b)呈现椭圆形，在梯度下降时会来回反弹。 最有利的方式是将特征值进行放缩，使得两个特征值在相同量级。

image.png|500

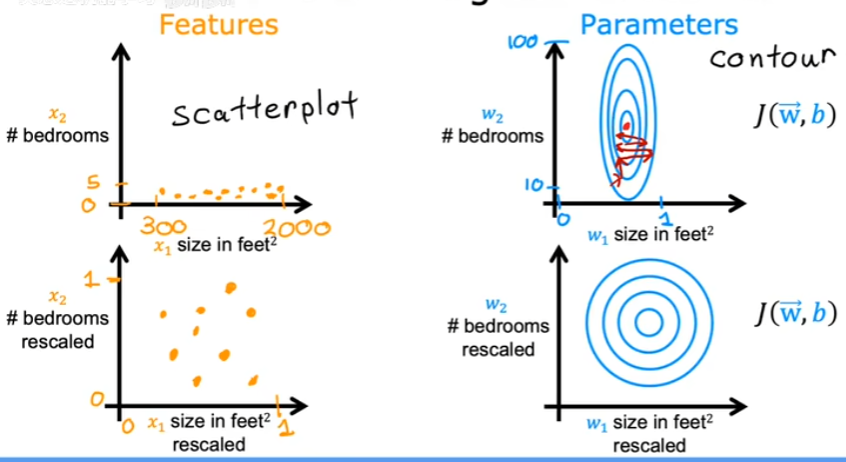
4.2 如何缩放

最值归一化

除以特征值取值的最大值，数据会映射到0~1之间。 \[x_{scale}=\frac{x-x_{min}}{x_{max}-x_{min}}\] 最值归一化只适用于有明显边间的情况。

均值归一化

\[x_{scale}=\frac{x-\mu}S\] 其中\(x\)为要归一化的值，\(x_{scale}\)为归一化之后的值。\(\mu\) 为样本的平均值，\(S\)为样本的标准差。

均值方差归一化

\[Y_i=\sigma\cdot X_i+\mu \] 其中，X为标准正态分布中的元素，\(\mu\)为平均值，\(\sigma\)为标准差。

4.3 学习曲线

可以判断何时停止训练特定模拟

image.png|500

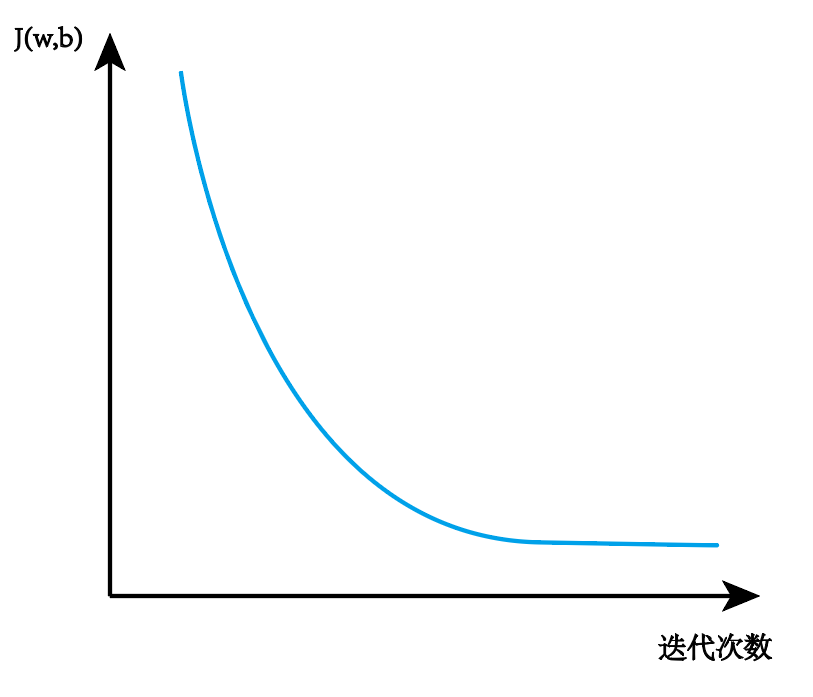
4.4 学习率选择

一个小的学习率，J应该是持续减小的。 在选择学习率时，可从小的开始，每次增加10倍改变，如0.001、0.01、0.1、1、10...