Ls-Dyna学习笔记

本文最新更新于 2025/03/05 下午

1、基础知识

1.1 关键字对应

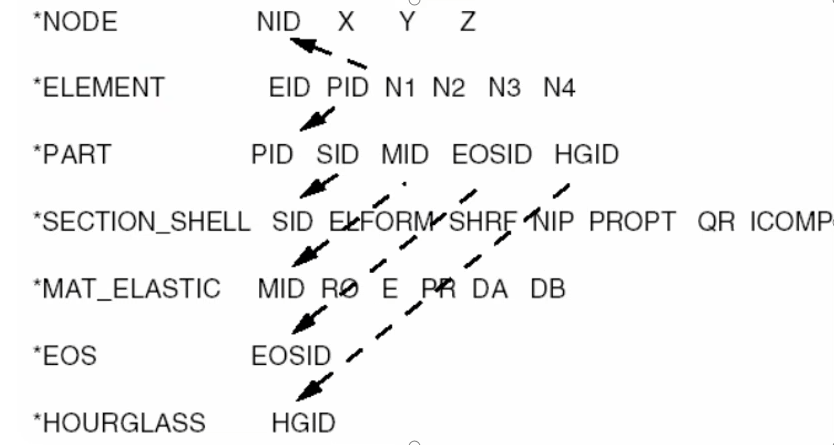
1.2 单位换算

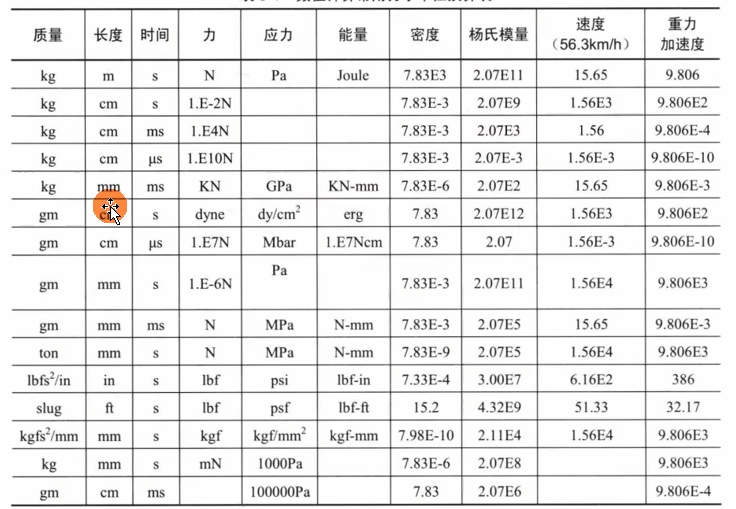
1.3 流程

1. 模型构建
2. 材料定义
3. 单元算法定义
4. 状态方程控制
5. 属性赋予
6. 连接关系设置
7. 边界与载荷条件工
8. 求解设置
9. 求解
10. 结果解读

2、关键字

2.1 Johnson_Cook

JC模型可处理应变和温度敏感塑性，有时用于处理应变率变化范围较大，由于塑性加热导致温度上升，从而引起材料软化的问题。如果热效应和损伤不重要，我们推荐使用价格低廉得多的 MAT_SIMPLIFIED_- JOHNSON_COOK模型。

JC模型在较低应变速率下，甚至在准静态条件下仍然有效。直到较低的应变速率，甚至进入准静态状态。典型应用典型应用包括爆炸性金属成型、弹道穿透和冲击。

解释含义

1. MID：唯一标识
2. RO：密度
3. G：剪切模量。G 对于 solids、2D shell 13-15 和 tshell 3 5 7有效，其他材料可忽略。
4. E：杨氏模量。
5. PR：泊松比
6. DTF：自动删除元素（壳元素）的最小时间步长。当求解时间步长低于 DTF × TSSFAC时，元素将被删除。
7. VP：针对速率效应方程
   1. EQ.0.0：比例屈服应力
   2. EQ.1.0：粘塑性方程
8. RATEOP：应变速率项的形式。如果VP为0，此项可忽略。
   1. EQ.0.0: Log-linear Johnson-Cook (default)
   2. EQ.1.0: Log-quadratic Huh-Kang (2 parameters)
   3. EQ.2.0: Exponential Allen-Rule-Jones
   4. EQ.3.0: Exponential Cowper-Symonds (2 parameters)
   5. EQ.4.0: Nonlinear rate coefficient (2 parameters)
   6. EQ.5.0: Log-exponential Couque (4 parameters)

      

9. A、B、C、D、m：求解流动应力
10. TM：融化温度
11. TR：室温
12. EPS0：准静态阈值应变率（见备注 1）。理想情况下，该值代表无需对流动应力进行速率调整的最高应变速率，以\([时间]^{-1}\)为单位输入。最高应变率，并以\([时间]^{-1}\)为单位输入。例如，如果应变速率对流动应力的影响在应变速率大于\(10^{-2}\)例如，如果应变速率大于 \(10^{-2}s^{-1}\)时，流动应力的应变速率效应才开始显现，模型输入的单位系统为 {kg、mm、ms}，则 EPSO 应设置为 \(10^{-5}\)
13. CP：比热
14. PC：拉伸失效应力或拉伸压力截止值
15. SPALL：
    1. Spall类型
       1. EQ.0.0: Set to “2.0” (default).
       2. EQ.1.0: 拉伸压力受PC限制, p总是大于PC
    2. 壳元素的特定行为
       1. EQ.2.0： 当 $_{max} ≥ -PC $ 时，壳元素被删除。
       2. EQ.3.0： 当 $p < PC $ 时，壳元素被删除。
    3. Solid特定行为
       1. EQ.2.0： 当 $_{max} ≥ -PC $ 时，拉应力重置为0。
       2. EQ.3.0： 当 $p < PC $ 时，拉应力重置为0。
16. IT：塑性应变迭代选项。此输入仅适用于实体元素，因为壳元素始终需要进行迭代平面应力条件
    1. EQ.0.0: 无迭代 (default)
    2. EQ.1.0: 塑性应变的精确迭代解决方案
17. D1-D4：失效参数，如果D30，则为绝对值
18. D5：失效参数
19. EROD：侵蚀标识
    1. EQ.0.0: Element erosion allowed (default).
    2. NE.0.0: 元件无侵蚀；元件失效时偏差应力设为零
20. EFMIN：断裂处计算应变的下限
21. NUMINT：在删除壳元素之前必须失效的贯通厚度积分点数。
22. C2/P/XNP：应变速率参数

    

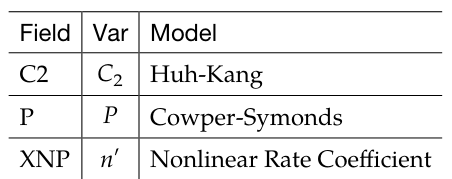
23. K：Couque项的应变速率参数
24. EPS1：表征过渡的Couque项的参考应变速率。介于热激活状态和粘性状态之间。输入的单位为[time]−1。

10、 案例

10.1、 小球跌落分析