JC方程
本文最新更新于 2025/03/12 晚上
1 材料演变过程
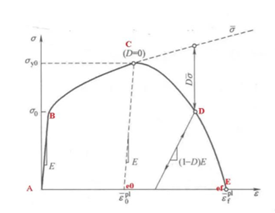
图中AB段为弹性段,B点为屈服点,BC为塑性段,C点为损伤起始点(失效点,此时损伤变量D=0),CE为损伤演化阶段(在此段材料即发生屈服应力软化和弹性退化,其弹模为(1-D)*E),E点为完全破坏点(弹性模量退化为0,损伤变量D=1)。
Abaqus中的损伤模型,即是要确定图中的损伤开始点C即后续的损伤演化阶段CE。
2 JC损伤模型
损伤开始时的等效塑性应变表达式为
\[\overline{\varepsilon}_{D}^{pl}=\left[d_{1}+d_{2}\exp\left(-d_{3}\eta\right)\right]\left[1+d_{4}\ln\left(\frac{\dot{\frac{\cdot}{\varepsilon}}^{pl}}{\dot{\varepsilon}_{0}}\right)\right]\left(1+d_{5}\hat{\theta}\right)\]
第一项反映了应力三轴度的影响,将应力三轴度的影响表示为一个指数形式,通过\(d_2\)和\(d_3\)控制,相比于常用的等效应变破坏规则,能够有效反映拉压应力对失效的影响,拉伸时失效应变较小,而在压缩时,失效应变较大。第二项反映了应变速率的影响,同一应力状态,失效应变与应变率的对数成线性关系,通过参数\(d_4\)调整可以得到符合实际的应变率-失效应变关系。第三项是反映了温度的影响。
这里\(d_3\)为正值,因为在Abaqus中

在Abaqus中JC损伤模型只能用于显式算法中
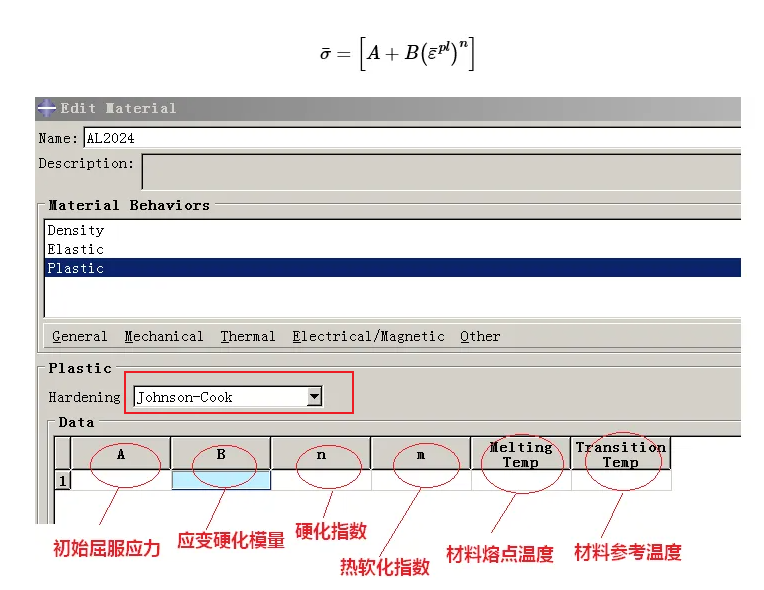
3 JC本构方程
\[\sigma=\left[A+B(\overline{\varepsilon^{pl}})^{n}\right]\left[1+C\ln\left(\frac{\dot{\frac{\cdot}{\varepsilon}}^{pl}}{\dot{\varepsilon}_{0}}\right)\right]\left(1-\hat{\theta}^{m}\right)\]
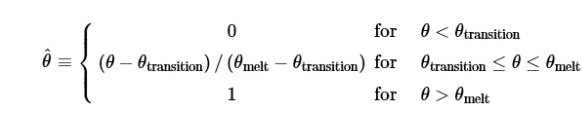
参数含义,A为静态屈服应力,B和n为材料应变硬化模量和硬化指数,C为材料应变率强化参数,m为材料热软化指数